Stellen Sie sich vor, Sie betreten eine riesige Bibliothek auf der Suche nach einem bestimmten Buch, aber ohne einen organisierten Katalog. Sie müssten jedes Regal durchsuchen, was Stunden oder sogar Tage dauern könnte. Wenn die Bibliothek jedoch über einen gut organisierten Katalog verfügt, können Sie einfach eine systematische Liste von Titeln, Autoren oder Themen konsultieren und das benötigte Buch schnell finden. Dieser strukturierte Ansatz ermöglicht es Ihnen, das Buch viel schneller und effizienter zu finden.

Ähnlich verhält es sich in einer Datenbank: Die Indizierung dient als dieser organisierte Katalog. Sie verbessert die Abfrageleistung (opens new window) durch die Schaffung eines Systems, das es der Datenbank ermöglicht, Datensätze schnell zu finden und abzurufen. Genauso wie ein Katalog Ihnen hilft, ein Buch schnell zu finden, hilft Ihnen ein Index, die benötigten Daten in der Datenbank viel schneller zu finden. Um dies zu erreichen, verwenden Datenbanken verschiedene Indizierungsalgorithmen (opens new window). Zum Beispiel ist die Hash-Indizierung effektiv für exakte Übereinstimmungsabfragen (opens new window), um spezifische Daten schnell zu finden. Eine andere Methode, die B-Tree-Indizierung, organisiert Daten auf strukturierte Weise, um Suchvorgänge zu beschleunigen.

Zusätzlich optimiert die Graph-Indizierung die Suche nach Daten mit komplexen Verbindungen, wie Beziehungen in sozialen Netzwerken. Ein Index fungiert als Straßenkarte in einer Datenbank und bietet schnellen Zugriff auf relevante Informationen (opens new window), ohne jeden Datensatz zu durchsuchen. Dies ist besonders wichtig für die Verwaltung großer Datensätze, bei denen sowohl Geschwindigkeit als auch Genauigkeit entscheidend sind.

B-Tree-Indizierungsalgorithmus

In der Datenbankverwaltung ist der B-Tree-Indizierungsalgorithmus entscheidend für die Optimierung von Such-, Einfüge- und Löschvorgängen. Sein Design und seine Eigenschaften machen ihn besonders effektiv für die effiziente Verwaltung großer Datensätze.

Funktionsweise des B-Tree-Index

Der B-Tree hält das Gleichgewicht aufrecht, indem er Knoten erlaubt, mehrere Kinder zu haben, im Gegensatz zu binären Suchbäumen (opens new window), die in der Regel nur zwei Kindknoten haben. Dieses Design ermöglicht es jedem Knoten, mehrere Schlüssel und Zeiger auf seine Kindknoten zu speichern, wodurch sichergestellt wird, dass alle Blattknoten auf der gleichen Tiefe bleiben und ein effizienter Zugriff auf Daten ermöglicht wird.

Diese Merkmale tragen zu den Schlüsseleigenschaften der B-Tree-Indizierung bei. Mit seiner ausgewogenen Struktur garantiert ein B-Tree eine Zeitkomplexität von O(log n) für Such-, Einfüge- und Löschvorgänge. Jeder Knoten kann zwischen t-1 und 2t-1 Schlüssel und zwischen t und 2t Kindknoten halten, was flexiblen Speicherplatz bietet. Dieses Gleichgewicht stellt sicher, dass die Höhe des Baums logarithmisch zur Anzahl der Schlüssel bleibt, was effiziente Operationen auch bei großen Datensätzen ermöglicht. Darüber hinaus ermöglichen die sortierten Schlüssel innerhalb der Knoten effiziente Bereichsabfragen und geordnete Traversierungen, was die Leistung des Baums weiter verbessert.

Lassen Sie uns dies anhand eines Beispiels verdeutlichen.

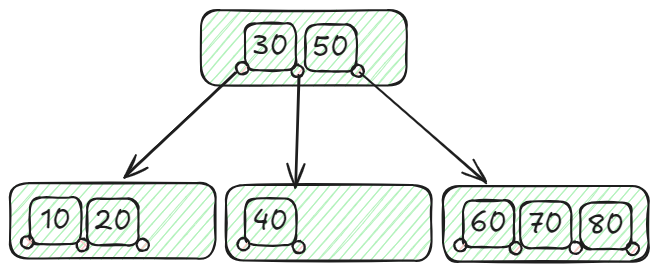
Nehmen wir an, wir haben eine Studentendatenbank, in der wir effizient nach Studentenakten anhand ihrer IDs suchen müssen. Angenommen, wir haben die folgenden Studenten-IDs zum Indizieren: 10, 20, 30, 40, 50, 60, 70 und 80. Wir erstellen einen B-Tree mit einem Mindestgrad (t) von 2.

In diesem B-Tree hält der primäre Knoten zwei Schlüssel (30 und 50), was zu drei Nachfolgeknoten führt: Der linke Knoten enthält IDs unter 30 (10, 20), der mittlere Knoten enthält IDs im Bereich von 30 bis 50 (40) und der rechte Knoten enthält IDs über 50 (60, 70, 80). Diese Organisation ermöglicht eine effektive Handhabung und Abruf von Studenten-IDs mithilfe der B-Tree-Datenstruktur. Um beispielsweise die ID 40 zu finden, beginnen Sie an der Wurzel und stellen fest, dass 40 zwischen 50 und 30 liegt. Sie gehen daher zum mittleren Kindknoten mit der ID 40. Diese gut ausbalancierte Organisation garantiert effiziente Such-, Einfüge- und Löschfunktionen mit einer Zeitkomplexität (opens new window) von O(log n).

Vorteile der B-Tree-Indizierung

Die B-Tree-Indizierung wird aufgrund ihrer Flexibilität und Effizienz bei der Verwaltung geordneter Daten sehr geschätzt. Die wichtigsten Vorteile sind:

1. Effiziente gefilterte Suchen: Die Fähigkeit, Knoten basierend auf bestimmten Kriterien schnell einzugrenzen, kombiniert mit der ausgewogenen und sortierten Natur, macht B-Trees besonders effektiv für gefilterte Suchen. Diese Effizienz bei der Handhabung komplexer Filter hilft, eine hohe Leistung bei großen Datensätzen aufrechtzuerhalten.
2. Konsistente Leistung: Die ausgewogene Natur von B-Trees gewährleistet, dass Such-, Einfüge- und Löschvorgänge eine vorhersehbare Leistung haben, in der Regel mit einer Zeitkomplexität von O(log n). Dieses Gleichgewicht hilft, die Effizienz auch bei wachsenden Datensätzen aufrechtzuerhalten.
3. Effiziente dynamische Aktualisierungen: B-Trees eignen sich gut für Datenbanken, in denen häufige Einfügungen und Löschungen auftreten (opens new window). Ihre Fähigkeit, das Gleichgewicht zu halten und Suchpfade zu optimieren, macht sie anpassungsfähig für dynamische Umgebungen, in denen sich die Datenstruktur kontinuierlich ändert.
4. Effektive Bereichsabfragen: Die sortierte Natur der Schlüssel in B-Trees ermöglicht effiziente Bereichsabfragen und geordnete Traversierungen. Diese Fähigkeit ist besonders nützlich für Operationen, die auf Daten innerhalb bestimmter Bereiche oder Sequenzen zugreifen müssen.
5. Optimierte Festplattennutzung: B-Trees reduzieren die Anzahl der für Suchoperationen erforderlichen Festplattenzugriffe, indem sie mehrere Schlüssel und Zeiger pro Knoten speichern. Dieses Design minimiert Festplatten-E/A-Operationen und verbessert die Leistung bei großen Datensätzen.

Einschränkungen der B-Tree-Indizierung

Trotz ihrer Stärken ist die B-Tree-Indizierung nicht immer die beste Wahl in jedem Szenario. Beachten Sie die folgenden Einschränkungen:

1. Skalierbarkeitsprobleme bei hochdimensionalen Daten: Mit zunehmender Dimensionalität der Vektoren kann die Leistung von B-Trees abnehmen. Dies macht sie weniger geeignet für Datenbanken, bei denen der Großteil der Daten hochdimensional ist.
2. Overhead in statischen Umgebungen: Für Datensätze, die überwiegend statisch oder schreibgeschützt sind, kann der mit der Aufrechterhaltung der ausgewogenen Struktur eines B-Trees verbundene Overhead die Leistungsvorteile überwiegen. In solchen Fällen können einfachere Indizierungsmethoden effizienter sein.
3. Komplexität und Speichernutzung: Die Implementierung und Verwaltung eines B-Trees kann im Vergleich zu einfacheren Datenstrukturen komplex sein. Darüber hinaus kann die Notwendigkeit, mehrere Schlüssel und Zeiger pro Knoten zu speichern, zu einer höheren Speichernutzung führen, was in speicherbeschränkten Umgebungen berücksichtigt werden sollte.
4. Höhere Speichernutzung: Die Notwendigkeit, mehrere Schlüssel und Zeiger pro Knoten in einem B-Tree zu speichern, kann zu einer höheren Speichernutzung führen, was in Vektor-Datenbanken mit großen Datensätzen ein Problem sein kann.

Datenbankadministratoren wählen oft zwischen B-Trees und hashbasierten Indizes basierend auf ihren Anforderungen aus. B-Trees eignen sich hervorragend für relationale Datenbanken, in denen geordnete Daten und Bereichsabfragen in niedrigdimensionalen Räumen effizient verwaltet werden und die Reihenfolge für traditionelle Operationen beibehalten wird.

In Vektor-Datenbanken, die hochdimensionale Daten verarbeiten (wie sie in KI und maschinellem Lernen verwendet werden), haben B-Trees aufgrund des Fluchs der Dimensionalität Schwierigkeiten. Mit zunehmender Dimensionalität werden B-Trees weniger effektiv, da sich die Daten gleichmäßiger verteilen und die Partitionierung schwierig wird. In solchen Fällen bietet die hashbasierte Indizierung eine überzeugende Alternative, über die wir als Nächstes sprechen werden, und kann eine bessere Leistung für hochdimensionale Datensätze bieten.

Hash-Indizierungsalgorithmus

Die Hash-Indizierung ist eine Technik, die entwickelt wurde, um die Sucheffizienz zu verbessern, insbesondere in hochdimensionalen Kontexten wie Vektor-Datenbanken. Sie funktioniert anders als B-Trees und ist besonders nützlich für die Verwaltung großer und komplexer Datensätze.

Funktionsweise der Hash-Indizierung

Die Hash-Indizierung verwendet eine Hash-Funktion (opens new window), um Schlüssel auf bestimmte Positionen in einer Hashtabelle abzubilden, was eine effiziente Datenabfrage (opens new window) ermöglicht. Im Gegensatz zu B-Trees, die eine ausgewogene Struktur aufrechterhalten, bieten Hash-Indizes eine konstante Zeitkomplexität von O(1) für Such-, Einfüge- und Löschvorgänge, was sie ideal für exakte Übereinstimmungsabfragen macht. Die Hash-Funktion wandelt einen Schlüssel in einen Hash-Code um, um seinen Index in der Hashtabelle zu bestimmen, während Eimer Einträge an jedem Index speichern. Techniken zur Behandlung von Kollisionen, wie Verkettung (verkettete Listen) oder offenes Adressieren (Sondieren), verwalten Fälle, in denen mehrere Schlüssel auf denselben Index gehasht werden.

In Vektor-Datenbanken wird die Hash-Indizierung für hochdimensionale Daten angepasst. Mehrere Hash-Funktionen verteilen Vektoren auf verschiedene Hasheimer. Während einer Suche nach dem nächsten Nachbarn werden Vektoren aus relevanten Eimern abgerufen und mit dem Abfragevektor verglichen. Die Effektivität der Methode hängt von der Qualität der Hash-Funktionen und davon ab, wie gut sie die Vektoren auf die Eimer verteilen. Die Hash-Indizierung verbessert die Sucheffizienz für exakte Übereinstimmungen, eignet sich jedoch weniger für Bereichsabfragen oder die geordnete Datenabfrage.

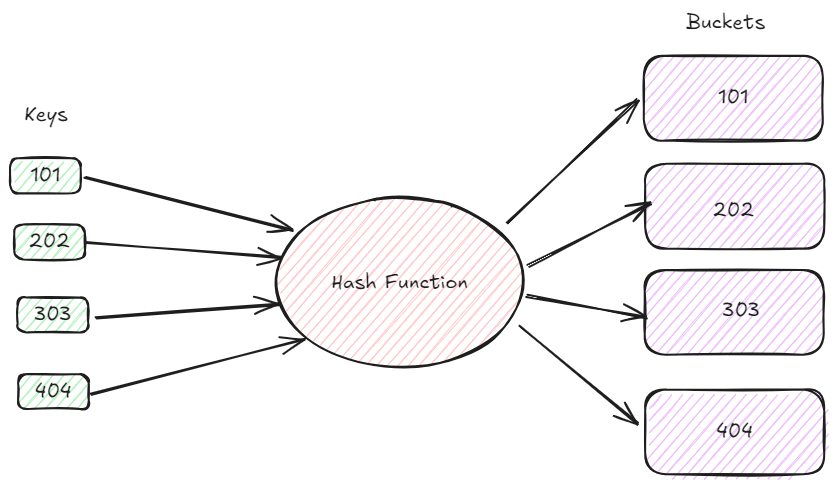
Nehmen wir nun ein Beispiel einer Bibliotheksdatenbank, in der wir effizient nach Buchdatensätzen anhand ihrer eindeutigen IDs suchen müssen. Angenommen, wir haben die folgenden Buch-IDs zum Indizieren: 101, 202, 303 und 404.

Dieses Diagramm zeigt die grundlegende Idee der Hash-Indizierung. Wir beginnen mit einer Sammlung von Buch-IDs, die als unsere Schlüssel dienen. Die Schlüssel durchlaufen eine Hash-Funktion, die sie in numerische Werte umwandelt. Diese Hash-Werte, als solche bezeichnet, bestimmen den Behälter, in dem die zugehörigen Buchdaten platziert werden. Idealerweise verteilt die Hash-Funktion die Schlüssel gleichmäßig auf die Eimer, um Kollisionen zu reduzieren. In diesem Fall ist jede Buch-ID einem eigenen Eimer zugeordnet, was eine einwandfreie Hash-Verteilung zeigt. In realen Situationen treten jedoch häufig Kollisionen auf und erfordern zusätzliche Methoden wie Verkettung oder offenes Adressieren, um sie erfolgreich zu verwalten.

Vorteile der Hash-Indizierung

1. Schnelle Suche: Die Hash-Indizierung bietet eine durchschnittliche konstante Zeitkomplexität O(1) für Suchoperationen, was sie für exakte Übereinstimmungsabfragen äußerst effizient macht.
2. Einfache Struktur: Die Struktur der Hashtabelle ist einfach, was die Implementierung und Verwaltung im Vergleich zu komplexeren Strukturen wie B-Trees vereinfacht.
3. Effizient für Punktanfragen: Die Hash-Indizierung eignet sich hervorragend für Szenarien, in denen Abfragen auf exakten Übereinstimmungen basieren, z. B. das Abrufen eines Datensatzes anhand eines eindeutigen Identifikators.

Einschränkungen der Hash-Indizierung

1. Ineffizient für Bereichsabfragen: Die Hash-Indizierung eignet sich nicht gut für Bereichsabfragen oder den Zugriff auf geordnete Daten, da die Hash-Funktion die Reihenfolge der Schlüssel nicht beibehält.
2. Overhead bei der Behandlung von Kollisionen: Die Behandlung von Kollisionen kann Overhead verursachen, insbesondere wenn die Hashtabelle nicht gut dimensioniert ist oder wenn Kollisionen häufig auftreten.
3. Feste Tabellengröße: Hashtabellen haben oft eine feste Größe, und das Ändern ihrer Größe kann komplex und kostspielig sein. Dies kann zu Leistungseinbußen führen, wenn die Tabelle überlastet wird.
4. Mangelnde Flexibilität: Im Gegensatz zu B-Trees unterstützen Hash-Indizes keine effizienten Bereichsabfragen oder geordneten Traversierungen, was für Anwendungen, die solche Operationen erfordern, ein erheblicher Nachteil sein kann.

Während die Hash-Indizierung für schnelle exakte Übereinstimmungsabfragen gut geeignet ist, kann sie bei hochdimensionalen Daten Schwierigkeiten haben. Für effiziente Approximationsnachbarschaftssuchen (ANN) bietet die Graph-Indizierung mit dem HNSW (Hierarchical Navigable Small World)-Algorithmus eine leistungsstarke Alternative, die komplexe, hochdimensionale Vektoren effektiv verwaltet.

Boost Your AI App Efficiency now

Sign up for free to benefit from 150+ QPS with 5,000,000 vectors

Free Trial

Explore our product

Graph-Indizierung

Die Graph-Indizierung ist sehr nützlich für die Handhabung komplexer Datenvernetzungen oder Beziehungen, wie soziale Verbindungen oder Empfehlungssysteme. Die Graph-Indizierung ist im Gegensatz zu linearen Datenstrukturen wie B-Trees oder Hashtabellen speziell darauf ausgelegt, Graphdaten effektiv zu handhaben und abzurufen, bei denen die Verbindungen zwischen Entitäten eine gleichwertige Bedeutung wie die Entitäten selbst haben.

In modernen Vektor-Datenbanken werden graphbasierte Indizierungsmethoden (opens new window) wie HNSW (Hierarchical Navigable Small World) (opens new window) häufig für Approximationsnachbarschaftssuchen (ANN) (opens new window) verwendet, insbesondere in hochdimensionalen Räumen. Diese fortschrittlichen Techniken sind darauf ausgelegt, große und komplexe Datensätze effizient zu durchsuchen.

Funktionsweise der Graph-Indizierung

Die Graph-Indizierung umfasst die Erstellung von Strukturen, die das schnelle Auffinden von Knoten (Vertices) und Kanten (Verbindungen) basierend auf bestimmten Abfragen ermöglichen. Der Indizierungsprozess kann sich auf verschiedene Aspekte des Graphen konzentrieren, wie z. B. Knotenbezeichnungen, Kantentypen oder die kürzesten Pfade zwischen Knoten. Es wurden mehrere Graph-Indizierungsmethoden entwickelt, um verschiedene Arten von Abfragen zu optimieren:

1. Pfadindizierung: Diese Methode indiziert spezifische Pfade im Graphen, um das Auffinden häufiger Muster oder Pfade zwischen Knoten zu beschleunigen. Sie ist besonders nützlich für Abfragen, bei denen der Graph durchsucht werden muss, um Beziehungen oder Verbindungen zu finden.
2. Teilgraphindizierung: Bei diesem Ansatz werden häufige Teilgraphen (kleinere Komponenten des Gesamtgraphen) indiziert, um effiziente Suchen nach bestimmten Mustern oder Strukturen innerhalb eines größeren Graphen zu ermöglichen.
3. Nachbarschaftsindizierung: Diese Methode konzentriert sich auf die Indizierung der unmittelbaren Nachbarn jedes Knotens, was für Abfragen nützlich ist, die Verbindungen oder Beziehungen direkt mit einem bestimmten Knoten erkunden müssen.

HNSW (Hierarchical Navigable Small World)

HNSW ist ein auf Graphen basierender Algorithmus, der speziell entwickelt wurde, um nächste Nachbarn in hochdimensionalen Vektorräumen effizient zu finden. Das Hauptkonzept von HNSW besteht darin, mehrere hierarchische Ebenen aufzubauen, wobei jede Ebene einen Graphen darstellt, der Knoten (Datenpunkte) basierend auf ihrer Nähe verbindet. Die oberen Ebenen geben eine allgemeine Zusammenfassung, während die unteren Ebenen detailliertere Informationen liefern.

In der Praxis startet der HNSW-Algorithmus bei einer Suche in der obersten Ebene und navigiert durch den Graphen, indem er allmählich zu den unteren Ebenen absteigt, wo die Suche präziser wird. Dieser hierarchische Ansatz reduziert den Suchraum erheblich und ermöglicht es, nächste Nachbarn auch in sehr großen Datensätzen schnell abzurufen.

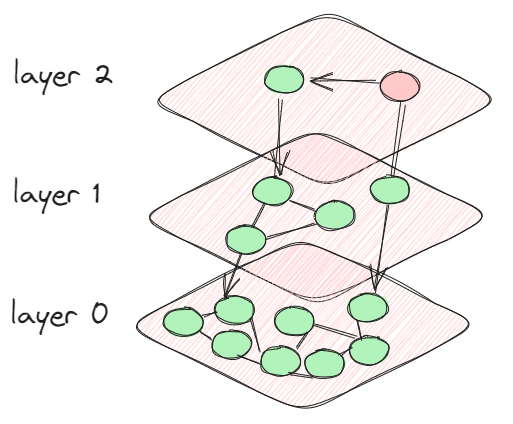
Stellen Sie sich vor, Sie suchen nach ähnlichen Bildern in einer großen Datenbank visueller Daten. Jedes Bild wird durch einen hochdimensionalen Vektor repräsentiert (z. B. extrahierte Merkmale aus einem neuronalen Netzwerk). HNSW ermöglicht es Ihnen, Bilder, die dem gegebenen Suchbild am nächsten kommen, schnell zu finden, indem Sie den hierarchischen Graphen durchlaufen und mit einer breiten Suche in den oberen Ebenen beginnen und sich allmählich den engsten Übereinstimmungen in den unteren Ebenen nähern. Graph-Indizierungsalgorithmen wie HNSW sind darauf ausgelegt, die Rechenkosten solcher Traversierungen zu minimieren, insbesondere in großen Graphen, in denen Millionen von Knoten und Kanten vorhanden sein können. Der Indizierungsprozess verbessert die Abfrageleistung erheblich, indem er sich auf relevante Teile des Graphen konzentriert.

Vorteile der Graph-Indizierung mit HNSW

1. Optimiert für komplexe Beziehungen: Die Graph-Indizierung eignet sich hervorragend für die Verwaltung und Abfrage von Daten mit komplexen Beziehungen, wie sozialen Netzwerken, bei denen Verbindungen zwischen Entitäten entscheidend sind.
2. Effiziente Traversierung für ANN-Suchen: HNSW ist äußerst effizient bei der Durchführung von Approximationsnachbarschaftssuchen, die für Aufgaben wie Bildsuche, Empfehlungssysteme und andere Anwendungen mit hochdimensionalen Daten entscheidend sind.
3. Skalierbarkeit: HNSW skaliert gut mit großen Datensätzen und verarbeitet Millionen von Vektoren mit relativ geringer Latenz.
4. Flexibilität: HNSW kann für verschiedene Anwendungsfälle angepasst werden und bietet ein Gleichgewicht zwischen Suchgenauigkeit und Recheneffizienz.

Einschränkungen der Graph-Indizierung mit HNSW

1. Approximierte Ergebnisse: HNSW ist für Approximationsnachbarschaftssuchen ausgelegt, was bedeutet, dass nicht immer die genaueste Übereinstimmung zurückgegeben wird, obwohl in der Regel ein guter Kompromiss zwischen Geschwindigkeit und Genauigkeit geboten wird.
2. Komplexe Implementierung: Die Graph-Indizierung, einschließlich HNSW, ist im Vergleich zu traditionellen Indizierungsmethoden wie B-Trees oder Hash-Indizierung komplexer zu implementieren. Sie erfordert spezialisierte Algorithmen, die auf bestimmte Arten von Abfragen und Graphstrukturen zugeschnitten sind.
3. Ressourcenintensiv: Aufgrund der Komplexität von Graphdaten kann die Indizierung und Abfrage ressourcenintensiv sein und mehr Speicher und Rechenleistung erfordern.
4. Speichernutzung: Die mehrschichtige Graphstruktur von HNSW kann eine erhebliche Menge an Speicherplatz beanspruchen, was in ressourcenbeschränkten Umgebungen berücksichtigt werden sollte.

Während B-Trees und Hash-Indizierung für bestimmte Arten von Abfragen gut geeignet sind, haben sie Schwierigkeiten mit komplexen oder hochdimensionalen Daten. Graph-Indizierungsmethoden wie HNSW bewältigen diese Herausforderungen, indem sie effizient komplexe Verbindungen durchsuchen. Der Multi-Scale Tree Graph (MSTG) von MyScale (opens new window) geht noch einen Schritt weiter und kombiniert das Beste aus SQL und graphbasierten Techniken. MSTG verwendet eine Mischung aus hierarchischen Baumstrukturen und Graphtraversierung, um schnell und genau in großen, komplexen Datensätzen zu suchen. Diese Kombination macht es zu einem leistungsstarken Werkzeug für die Bewältigung der heutigen umfangreichen und komplexen Daten.

Multi-Scale Tree Graph (MSTG)

Der Multi-Scale Tree Graph (MSTG)-Algorithmus, entwickelt von MyScale (opens new window), ist eine fortschrittliche Indizierungstechnik, die die Einschränkungen herkömmlicher Vektor-Suchalgorithmen wie HNSW (Hierarchical Navigable Small World) (opens new window) und IVF (Inverted File Indexing) (opens new window) überwindet. MSTG eignet sich besonders gut für die Verarbeitung von groß angelegten, hochdimensionalen Vektordaten und bietet eine überlegene Leistung für Standard- und gefilterte Suchen.

Funktionsweise von MSTG

MSTG kombiniert die Vorteile der hierarchischen Baumclustering und der Graphtraversierung, um einen robusten und effizienten Suchmechanismus zu schaffen. Hier ist, wie es funktioniert:

1. Hierarchisches Baumclustering: In der Anfangsphase verwendet MSTG einen baumbasierten Clustering-Ansatz, um die Daten in Cluster zu organisieren. Diese hierarchische Struktur hilft dabei, den Suchraum zu reduzieren und den Abrufprozess schneller und effizienter zu gestalten.
2. Graphtraversierung: (opens new window) Sobald die Daten in Cluster organisiert sind, wendet MSTG Graphtraversierungstechniken an, um zwischen diesen Clustern zu navigieren. Dadurch können die nächsten Nachbarn schnell und genau abgerufen werden, auch in komplexen, hochdimensionalen Räumen.
3. Hybridansatz: Die hybride Natur von MSTG ermöglicht es ihm, sowohl dichte als auch spärliche Bereiche des Vektorraums effizient zu verwalten. Diese Anpassungsfähigkeit ist entscheidend für seine Leistung, insbesondere bei großen Datensätzen, bei denen herkömmliche Algorithmen möglicherweise Schwierigkeiten haben.

Überwindung der Einschränkungen anderer Algorithmen

MSTG behebt mehrere wichtige Einschränkungen bestehender Vektor-Suchalgorithmen:

1. Einschränkungen von HNSW: Während HNSW für ungefilterte Suchen effektiv ist, sinkt seine Leistung für gefilterte Suchen erheblich, insbesondere wenn das Filterverhältnis gering ist. MSTG überwindet dies, indem es auch unter restriktiven Filterbedingungen eine hohe Genauigkeit und Geschwindigkeit beibehält, dank seines kombinierten Baum- und graphbasierten Ansatzes.
2. Einschränkungen von IVF: IVF und seine Varianten können mit zunehmender Datensatzgröße einen erhöhten Indexspeicherbedarf und eine reduzierte Effizienz aufweisen. MSTG reduziert den Ressourcenverbrauch und behält auch bei massiven Datensätzen schnelle Suchzeiten bei.
3. Ressourceneffizienz: MSTG nutzt speicherressourcenschonende Speicherlösungen wie NVMe SSDs, um den Ressourcenverbrauch zu reduzieren, der IVF und HNSW normalerweise belastet. Dadurch wird es sowohl kosteneffektiv als auch skalierbar für groß angelegte Anwendungen.

MyScale (opens new window) optimiert die gefilterte Vektor-Suche (opens new window) mit dem einzigartigen MSTG-Algorithmus, der einen signifikanten Leistungssprung für Vektor-Suchaufgaben bietet, insbesondere in Szenarien mit großen und komplexen Datensätzen. Der hybride Ansatz und das ressourceneffiziente Design machen es zu einem leistungsstarken Werkzeug für moderne Vektor-Datenbanken und gewährleisten schnelle, genaue und skalierbare Suchfunktionen.

Join Our Newsletter

Subscribe

Die richtige Wahl für Ihre Datenbank treffen

Die Auswahl eines Indizierungsalgorithmus sollte an Ihre spezifischen Anforderungen angepasst werden und dabei den Datentyp, die Abfragehäufigkeit und die Leistungsanforderungen Ihrer Datenbank berücksichtigen. Wenn Ihre Datenbank beispielsweise häufig Bereichsabfragen durchführt oder effiziente Sortierfunktionen erfordert, könnte ein B-Tree-Index aufgrund seiner optimierten Struktur für solche Operationen besser geeignet sein. Wenn es jedoch hauptsächlich um exakte Übereinstimmungsabfragen und schnelle Nachschlagevorgänge geht, könnte ein Hash-Index in diesen Szenarien eine bessere Leistung bieten.

Zusammenfassend ist es wichtig, die charakteristischen Merkmale jedes Indizierungsalgorithmus zu verstehen, um eine fundierte Entscheidung zu treffen, die die Abfrageleistung basierend auf den einzigartigen Anforderungen Ihrer Datenbank optimiert.