In der modernen digitalen Ära sind personalisierte Empfehlungen entscheidend, um die Benutzerinteraktion zu verbessern. Zum Beispiel nutzt eine Musik-Streaming-Anwendung Ihre Hörgewohnheiten, um neue Songs vorzuschlagen, die Ihrem Geschmack, Genre oder Ihrer Stimmung entsprechen. Aber wie entscheiden diese Systeme, welche Songs am besten für Sie geeignet sind?
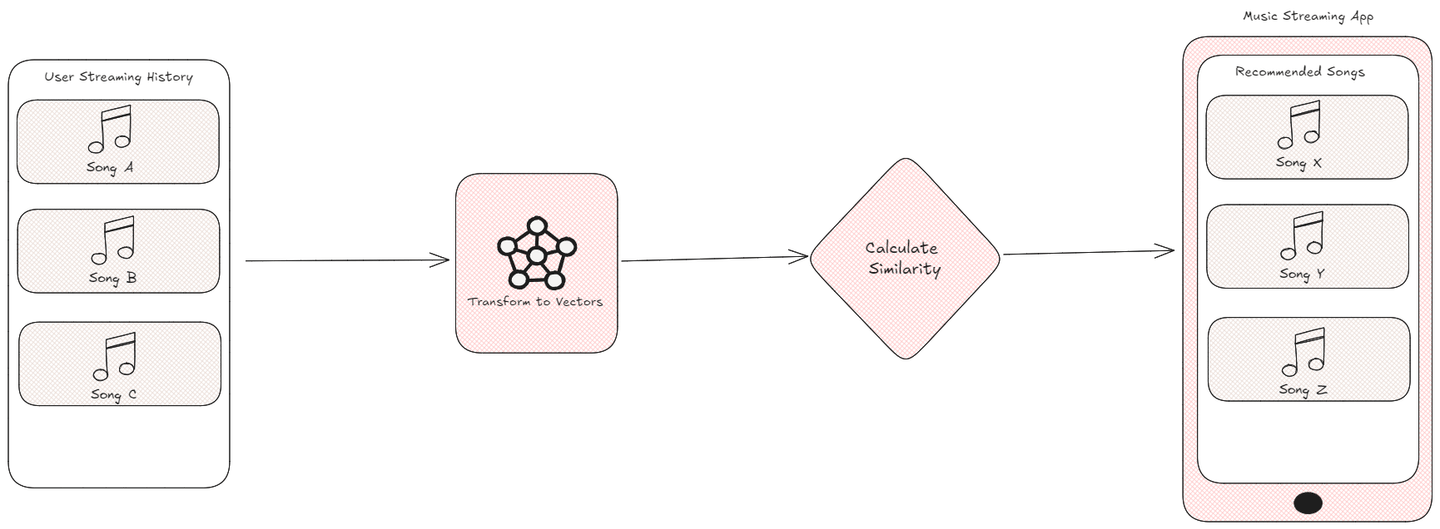
Die Antwort liegt darin, diese Datenpunkte in Vektoren umzuwandeln und ihre Ähnlichkeit mithilfe spezifischer Metriken zu berechnen. Durch den Vergleich der Vektoren, die Songs, Produkte oder Benutzerverhalten repräsentieren, können Algorithmen effektiv ihre eng verwandten Merkmale messen. Dieser Prozess ist grundlegend in den Bereichen maschinelles Lernen (opens new window) und künstliche Intelligenz (opens new window), wo Ähnlichkeitsmetriken Systemen ermöglichen, genaue Empfehlungen zu liefern, ähnliche Daten zu gruppieren und nächstgelegene Nachbarn zu identifizieren, um letztendlich eine personalisierte und ansprechende Benutzererfahrung zu schaffen.
# Was sind Ähnlichkeitsmetriken?
Ähnlichkeitsmetriken sind Instrumente, die verwendet werden, um den Grad der Ähnlichkeit oder Unähnlichkeit zwischen zwei Entitäten zu bestimmen. Diese Objekte können Textdokumente, Bilder oder Datenpunkte in einem Datensatz umfassen. Betrachten Sie Ähnlichkeitsmetriken als ein Werkzeug zur Bewertung der Nähe von Beziehungen zwischen Objekten. Sie spielen eine entscheidende Rolle in verschiedenen Bereichen wie dem maschinellen Lernen, indem sie Computern helfen, Muster in Daten zu erkennen, ähnliche Objekte zu gruppieren und Empfehlungen zu geben. Wenn Sie beispielsweise Filme entdecken möchten, die einem Film ähnlich sind, den Sie mögen, helfen Ähnlichkeitsmessungen dabei, dies zu bestimmen, indem sie die Merkmale verschiedener Filme untersuchen.
- Euklidischer Abstand: (opens new window) Dies misst den Abstand zwischen zwei Punkten im Raum, ähnlich wie die Messung der Luftlinie zwischen zwei Orten auf einer Karte. Es gibt Ihnen den genauen Abstand zwischen ihnen.
- Kosinus-Ähnlichkeit: (opens new window) Dies überprüft, wie ähnlich zwei Listen von Zahlen (wie Bewertungen oder Merkmale) sind, indem der Winkel zwischen ihnen betrachtet wird. Wenn der Winkel klein ist, bedeutet dies, dass die Listen sehr ähnlich sind, auch wenn sie unterschiedliche Längen haben. Es hilft Ihnen zu verstehen, wie eng zwei Dinge basierend auf ihrer Richtung verwandt sind.
Nun wollen wir beide im Detail untersuchen, um zu verstehen, wie sie funktionieren.
# Euklidischer Abstand
Der euklidische Abstand quantifiziert den Abstand zwischen zwei Punkten in einem mehrdimensionalen Raum, indem er ihre Trennung misst und die Ähnlichkeit basierend auf dem räumlichen Abstand aufdeckt. Diese Messung ist besonders wertvoll in Online-Shopping-Plattformen, die Kunden je nach ihrem Surf- und Kaufverhalten Produkte vorschlagen. Jedes Produkt kann hier als Punkt in einem mehrdimensionalen Raum dargestellt werden, wobei verschiedene Dimensionen Aspekte wie Preis, Kategorie und Benutzerbewertungen darstellen.
Das System berechnet den euklidischen Abstand zwischen Produktvektoren, wenn ein Benutzer bestimmte Artikel ansieht oder kauft. Wenn zwei Produkte in geringerem Abstand zueinander stehen, gelten sie als ähnlicher, was dem System dabei hilft, Artikel vorzuschlagen, die den Vorlieben des Benutzers nahe kommen.
# Formel:
Der euklidische Abstand d zwischen zwei Punkten A(x1,y1) und B(x2,y2) im zweidimensionalen Raum wird wie folgt berechnet:
Für den n-dimensionalen Raum generalisiert sich die Formel zu:
Die Formel berechnet den Abstand, indem sie die Quadratwurzel der Summe der quadrierten Differenzen zwischen jeder entsprechenden Dimension der beiden Punkte nimmt. Im Wesentlichen misst sie, wie weit die beiden Punkte in einer geraden Linie voneinander entfernt sind, was eine einfache Möglichkeit zur Bewertung der Ähnlichkeit darstellt.
# Beispielcode
Nun wollen wir ein Beispiel programmieren, das einen Graphen generiert, um den euklidischen Abstand zu berechnen:
import numpy as np
import matplotlib.pyplot as plt
# Definieren Sie zwei Punkte im 2D-Raum
Punkt_A = np.array([1, 2])
Punkt_B = np.array([2, 3])
# Berechnen Sie den euklidischen Abstand
euklidischer_abstand = np.linalg.norm(Punkt_A - Punkt_B)
# Erstellen Sie eine Abbildung und Achse
fig, ax = plt.subplots(figsize=(8, 8))
# Zeichnen Sie die Punkte
ax.quiver(0, 0, Punkt_A[0], Punkt_A[1], angles='xy', scale_units='xy', scale=1, color='r', label='Punkt A (1, 2)')
ax.quiver(0, 0, Punkt_B[0], Punkt_B[1], angles='xy', scale_units='xy', scale=1, color='b', label='Punkt B (2, 3)')
# Setzen Sie die Grenzen des Graphen
ax.set_xlim(0, 3)
ax.set_ylim(0, 4)
# Fügen Sie ein Gitter hinzu
ax.grid()
# Fügen Sie Beschriftungen hinzu
ax.annotate('A', Punkt_A, textcoords="offset points", xytext=(-10,10), ha='center', fontsize=12)
ax.annotate('B', Punkt_B, textcoords="offset points", xytext=(10,-10), ha='center', fontsize=12)
# Zeichnen Sie eine Linie, die den euklidischen Abstand darstellt
ax.plot([Punkt_A[0], Punkt_B[0]], [Punkt_A[1], Punkt_B[1]], 'k--', label='Euklidischer Abstand')
# Fügen Sie eine Legende hinzu
ax.legend()
# Fügen Sie Titel und Beschriftungen hinzu
ax.set_title(f'Euklidischer Abstand: {euklidischer_abstand:.2f}')
ax.set_xlabel('X-Achse')
ax.set_ylabel('Y-Achse')
# Zeigen Sie das Diagramm an
plt.show()
Bei Ausführung dieses Codes wird die folgende Ausgabe generiert.
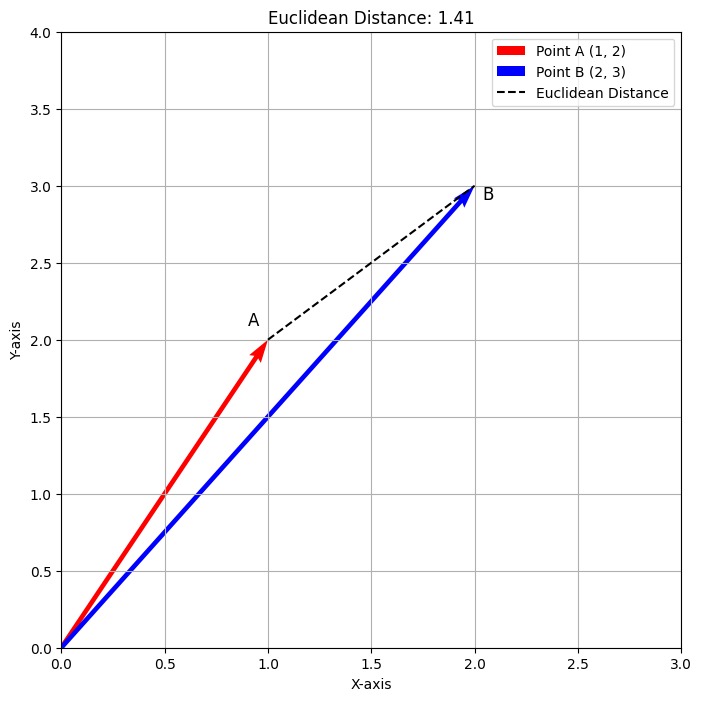
Das obige Diagramm veranschaulicht den euklidischen Abstand zwischen den Punkten A(1,2) und B(2,3). Der rote Vektor stellt Punkt A dar, der blaue Vektor stellt Punkt B dar und die gestrichelte Linie zeigt den Abstand von ungefähr 1,41 an. Diese Visualisierung veranschaulicht anschaulich, wie der euklidische Abstand den direkten Weg zwischen den beiden Punkten misst.
# Kosinus-Ähnlichkeit
Die Kosinus-Ähnlichkeit ist eine Metrik, die verwendet wird, um zu messen, wie ähnlich zwei Vektoren sind, unabhängig von ihrer Größe. Sie quantifiziert den Kosinus des Winkels zwischen zwei nicht-nullen Vektoren in einem n-dimensionalen Raum und gibt Einblick in ihre Richtungsähnlichkeit. Diese Messung ist besonders nützlich in Empfehlungssystemen, wie sie von Inhaltplattformen wie Netflix oder Spotify verwendet werden, wo sie bei der Empfehlung von Filmen oder Songs basierend auf den Benutzerpräferenzen hilft. In diesem Kontext kann jedes Element (z. B. ein Film oder ein Song) als Vektor von Merkmalen wie Genre, Bewertungen und Benutzerinteraktionen dargestellt werden.
Wenn ein Benutzer mit bestimmten Elementen interagiert, berechnet das System die Kosinus-Ähnlichkeit zwischen den entsprechenden Vektoren der Elemente. Wenn der Kosinuswert nahe bei 1 liegt, deutet dies auf einen hohen Grad an Ähnlichkeit hin und hilft der Plattform, Artikel vorzuschlagen, die den Interessen des Benutzers entsprechen.
# Formel:
Die Kosinus-Ähnlichkeit S zwischen zwei Vektoren A und B wird wie folgt berechnet:
Wo:
- A⋅B das Skalarprodukt der Vektoren ist.
- ∥A∥ und ∥B∥ die Beträge (oder Normen) der Vektoren sind.
Diese Formel berechnet den Kosinus des Winkels zwischen den beiden Vektoren und misst effektiv ihre Ähnlichkeit basierend auf der Richtung und nicht auf der Größe.
# Beispielcode
Nun wollen wir ein Beispiel programmieren, das die Kosinus-Ähnlichkeit berechnet und die Vektoren visualisiert:
import numpy as np
import matplotlib.pyplot as plt
# Definieren Sie zwei Vektoren im 2D-Raum
Vektor_A = np.array([1, 2])
Vektor_B = np.array([2, 3])
# Berechnen Sie die Kosinus-Ähnlichkeit
Skalarprodukt = np.dot(Vektor_A, Vektor_B)
Norm_A = np.linalg.norm(Vektor_A)
Norm_B = np.linalg.norm(Vektor_B)
Kosinus_Ähnlichkeit = Skalarprodukt / (Norm_A * Norm_B)
# Erstellen Sie eine Abbildung und Achse
fig, ax = plt.subplots(figsize=(8, 8))
# Zeichnen Sie die Vektoren
ax.quiver(0, 0, Vektor_A[0], Vektor_A[1], angles='xy', scale_units='xy', scale=1, color='r', label='Vektor A (1, 2)')
ax.quiver(0, 0, Vektor_B[0], Vektor_B[1], angles='xy', scale_units='xy', scale=1, color='b', label='Vektor B (2, 3)')
# Zeichnen Sie den Winkel zwischen den Vektoren
Winkel_Start = np.array([Vektor_A[0] * 0.7, Vektor_A[1] * 0.7])
Winkel_Ende = np.array([Vektor_B[0] * 0.7, Vektor_B[1] * 0.7])
ax.plot([Winkel_Start[0], Winkel_Ende[0]], [Winkel_Start[1], Winkel_Ende[1]], 'k--', color='gray')
# Beschriften Sie den Winkel und die Kosinus-Ähnlichkeit
ax.text(0.5, 0.5, f'Kosinus-Ähnlichkeit: {Kosinus_Ähnlichkeit:.2f}', fontsize=12, color='black', ha='center')
# Setzen Sie die Grenzen des Graphen
ax.set_xlim(0, 3)
ax.set_ylim(0, 4)
# Fügen Sie ein Gitter hinzu
ax.grid()
# Fügen Sie Beschriftungen für die Vektoren hinzu
ax.annotate('A', Vektor_A, textcoords="offset points", xytext=(-10, 10), ha='center', fontsize=12)
ax.annotate('B', Vektor_B, textcoords="offset points", xytext=(10, -10), ha='center', fontsize=12)
# Fügen Sie eine Legende hinzu
ax.legend()
# Fügen Sie Titel und Beschriftungen hinzu
ax.set_title('Kosinus-Ähnlichkeit Visualisierung')
ax.set_xlabel('X-Achse')
ax.set_ylabel('Y-Achse')
# Zeigen Sie das Diagramm an
plt.show()
Bei Ausführung dieses Codes wird die folgende Ausgabe generiert.
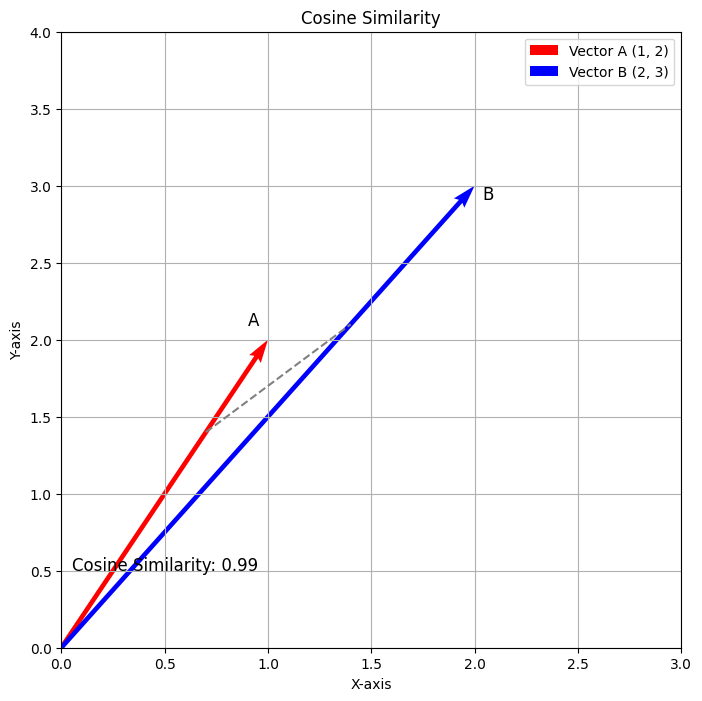
Das obige Diagramm veranschaulicht die Kosinus-Ähnlichkeit zwischen den Vektoren A(1,2) und B(2,3). Der rote Vektor stellt Vektor A dar und der blaue Vektor stellt Vektor B dar. Die gestrichelte Linie zeigt den Winkel zwischen den beiden Vektoren an, wobei die berechnete Kosinus-Ähnlichkeit ungefähr 0,98 beträgt. Diese Visualisierung veranschaulicht effektiv, wie die Kosinus-Ähnlichkeit die Richtungsbeziehung zwischen den beiden Vektoren misst.
# Verwendung von Ähnlichkeitsmetriken in Vektor-Datenbanken
Vektor-Datenbanken spielen eine entscheidende Rolle in Empfehlungssystemen und KI-gesteuerten Analysen, indem sie unstrukturierte Daten in hochdimensionale Vektoren für effiziente Ähnlichkeitssuchen umwandeln. Quantitative Messungen wie der euklidische Abstand und die Kosinus-Ähnlichkeit werden verwendet, um diese Vektoren zu vergleichen und es Systemen zu ermöglichen, geeignete Inhalte vorzuschlagen oder Unregelmäßigkeiten zu identifizieren. Zum Beispiel paaren Empfehlungssysteme Benutzerpräferenzen mit Artikelvektoren und bieten maßgeschneiderte Empfehlungen an.
MyScale (opens new window) nutzt diese Metriken, um seinen MSTG (Multi-Scale Tree Graph) (opens new window) Algorithmus anzutreiben, der Baum- und Graphstrukturen kombiniert, um äußerst effiziente Vektorsuchen durchzuführen, insbesondere in großen, gefilterten Datensätzen. MSTG ist besonders effektiv bei der Bearbeitung von gefilterten Suchen und übertrifft andere Algorithmen wie HNSW, wenn die Filterkriterien streng sind, was schnellere und präzisere nächstgelegene Nachbarschaftssuchen ermöglicht.
Der Metriktyp in MyScale ermöglicht es Benutzern, zwischen euklidischem (L2), Kosinus oder Innerem Produkt (IP) als Abstandsmetriken zu wechseln, je nach Art der Daten und dem gewünschten Ergebnis. Zum Beispiel wird in Empfehlungssystemen oder NLP-Aufgaben häufig die Kosinus-Ähnlichkeit verwendet, um Vektoren abzugleichen, während der euklidische Abstand für Aufgaben bevorzugt wird, die räumliche Nähe erfordern, wie Bild- oder Objekterkennung.
Durch die Integration dieser Metriken in seinen MSTG-Algorithmus optimiert MyScale Vektorsuchen über verschiedene Datenmodalitäten hinweg und eignet sich daher hervorragend für Anwendungen, die schnelle, genaue und skalierbare KI-gesteuerte Analysen erfordern.
# Fazit
Zusammenfassend spielen Ähnlichkeitsmessungen wie der euklidische Abstand und die Kosinus-Ähnlichkeit eine entscheidende Rolle im maschinellen Lernen, in Empfehlungssystemen und in KI-Anwendungen. Durch den Vergleich von Vektoren, die Datenpunkte repräsentieren, ermöglichen diese Metriken Systemen, Verbindungen zwischen Objekten aufzudecken und personalisierte Empfehlungen zu geben oder Muster in Daten zu erkennen. Der euklidische Abstand berechnet die lineare Entfernung zwischen Punkten, während die Kosinus-Ähnlichkeit die Richtungskorrelation untersucht, wobei jede Metrik je nach spezifischem Szenario unterschiedliche Vorteile bietet.
MyScale verbessert die Effektivität dieser Ähnlichkeitsmetriken durch seinen innovativen MSTG-Algorithmus, der sowohl die Geschwindigkeit als auch die Genauigkeit von Ähnlichkeitssuchen optimiert. Durch die Integration von Baum- und Graphstrukturen beschleunigt MSTG den Suchprozess, selbst bei komplexen, gefilterten Daten, was MyScale zu einer leistungsstarken Lösung für hochleistungsfähige KI-gesteuerte Analysen, die Handhabung großer Datenmengen und präzise, effiziente Vektorsuchen macht.




