Imagina entrar en una biblioteca enorme en busca de un libro específico, pero sin un catálogo organizado. Tendrías que recorrer cada estantería, lo que podría llevar horas o incluso días. Sin embargo, si la biblioteca está equipada con un catálogo bien organizado, simplemente puedes referirte a una lista sistemática de títulos, autores o temas y localizar rápidamente el libro que necesitas. Este enfoque estructurado hace que encontrar el libro sea mucho más rápido y eficiente.

De manera similar, en una base de datos, la indexación funciona como ese catálogo organizado. Mejora el rendimiento de las consultas (opens new window) al crear un sistema que permite a la base de datos localizar y recuperar registros rápidamente (opens new window). Al igual que un catálogo te ayuda a encontrar un libro rápidamente, un índice ayuda a la base de datos a encontrar los datos que necesitas mucho más rápido. Para lograr esto, las bases de datos utilizan diferentes algoritmos de indexación (opens new window). Por ejemplo, la indexación por hash es efectiva para consultas de coincidencia exacta (opens new window), encontrando rápidamente datos específicos. Otro método, la indexación B-Tree, organiza los datos de una manera estructurada que acelera las búsquedas.

Además, la indexación por grafos optimiza las búsquedas de datos con conexiones complejas, como las relaciones en redes sociales. Un índice actúa como un mapa en una base de datos, ofreciendo acceso rápido a información relevante (opens new window) sin tener que escanear cada registro. Esto es esencial para gestionar grandes conjuntos de datos donde tanto la velocidad como la precisión son críticas.

Algoritmo de indexación de árbol B

En la gestión de bases de datos, el algoritmo de indexación de árbol B es crucial para optimizar las operaciones de búsqueda, inserción y eliminación. Su diseño y propiedades lo hacen particularmente efectivo para administrar conjuntos de datos grandes de manera eficiente.

Cómo funciona el índice de árbol B

El árbol B mantiene el equilibrio al permitir que los nodos tengan múltiples hijos, a diferencia de los árboles de búsqueda binaria, que generalmente tienen solo dos nodos hijos. Este diseño permite que cada nodo almacene múltiples claves y punteros a sus nodos hijos, asegurando que todos los nodos hoja permanezcan a la misma profundidad y proporcionando un acceso eficiente a los datos.

Estas características contribuyen a las propiedades clave de la indexación de árbol B. Con su estructura equilibrada, un árbol B garantiza una complejidad temporal de O(log n) para las operaciones de búsqueda, inserción y eliminación. Cada nodo puede contener entre t-1 y 2t-1 claves y entre t y 2t hijos, ofreciendo un almacenamiento flexible. Este equilibrio asegura que la altura del árbol permanezca logarítmica en relación con el número de claves, lo que admite operaciones eficientes incluso con conjuntos de datos grandes. Además, las claves ordenadas dentro de los nodos facilitan las consultas de rango eficientes y los recorridos ordenados, mejorando aún más el rendimiento del árbol.

Veámoslo con la ayuda de un ejemplo.

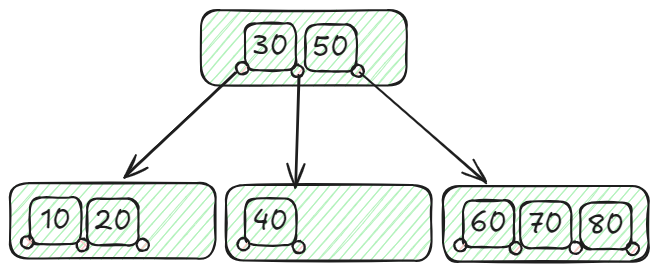
Considera una base de datos de estudiantes en la que necesitamos buscar eficientemente registros de estudiantes por sus ID. Supongamos que tenemos los siguientes ID de estudiantes para indexar: 10, 20, 30, 40, 50, 60, 70 y 80. Construimos un árbol B con un grado mínimo (t) de 2.

Dentro de este árbol B, el nodo principal tiene dos claves (30 y 50), lo que lleva a tres nodos hijos: el nodo izquierdo que preserva los ID por debajo de 30 (10, 20), el nodo central que aloja los ID que van desde 30 hasta 50 (40), y el nodo derecho que almacena los ID que superan los 50 (60, 70, 80). Esta organización permite el manejo y la recuperación efectiva de los ID de los estudiantes utilizando la estructura de datos del árbol B. Por ejemplo, para localizar el ID 40, comenzarías en la raíz y observarías que 40 se encuentra entre 50 y 30. Por lo tanto, procederías al nodo hijo central que contiene 40. Esta organización bien equilibrada garantiza funciones de búsqueda, inserción y eliminación eficientes con una complejidad temporal (opens new window) de O(log n).

Ventajas de la indexación de árbol B

La indexación de árbol B es muy valorada por su flexibilidad y eficiencia en la gestión de datos ordenados. Las principales ventajas incluyen:

1. Búsquedas filtradas eficientes: La capacidad de reducir rápidamente los nodos en función de criterios específicos, combinada con la naturaleza equilibrada y ordenada, hace que los árboles B sean particularmente eficientes para búsquedas filtradas. Esta eficiencia en el manejo de filtros complejos ayuda a mantener un alto rendimiento en conjuntos de datos grandes.
2. Rendimiento constante: La naturaleza equilibrada de los árboles B garantiza que las operaciones de búsqueda, inserción y eliminación tengan un rendimiento predecible, generalmente con una complejidad temporal de O(log n). Este equilibrio ayuda a mantener la eficiencia incluso a medida que el conjunto de datos crece.
3. Actualizaciones dinámicas eficientes: Los árboles B son adecuados para bases de datos donde ocurren inserciones y eliminaciones frecuentes. Su capacidad para mantener el equilibrio y optimizar las rutas de búsqueda los hace adaptables a entornos dinámicos, donde la estructura de datos cambia continuamente.
4. Consultas de rango eficientes: La naturaleza ordenada de las claves dentro de los árboles B admite consultas de rango eficientes y recorridos ordenados. Esta capacidad es particularmente útil para operaciones que requieren acceder a datos dentro de rangos o secuencias específicas.
5. Uso optimizado de disco: Los árboles B reducen la cantidad de accesos a disco necesarios para las operaciones de búsqueda almacenando múltiples claves y punteros por nodo. Este diseño minimiza las operaciones de E/S de disco, mejorando el rendimiento para conjuntos de datos grandes.

Limitaciones de la indexación de árbol B

A pesar de sus fortalezas, la indexación de árbol B no siempre es la mejor opción en todos los escenarios. Considera las siguientes limitaciones:

1. Problemas de escalabilidad con datos de alta dimensionalidad: A medida que aumenta la dimensionalidad de los vectores, el rendimiento de los árboles B puede degradarse. Esto los hace menos adecuados para bases de datos donde la mayoría de los datos son de alta dimensionalidad.
2. Overhead en entornos estáticos: Para conjuntos de datos que son predominantemente estáticos o de solo lectura, el overhead asociado con el mantenimiento de la estructura equilibrada de un árbol B puede superar sus beneficios de rendimiento. En tales casos, métodos de indexación más simples podrían ser más eficientes.
3. Complejidad y uso de memoria: Implementar y gestionar un árbol B puede ser complejo en comparación con estructuras de datos más simples. Además, la necesidad de almacenar múltiples claves y punteros por nodo puede llevar a un mayor uso de memoria, lo que podría ser una consideración en entornos con restricciones de memoria.
4. Mayor uso de memoria: La necesidad de almacenar múltiples claves y punteros por nodo en un árbol B puede llevar a un mayor uso de memoria, lo que podría ser una preocupación en bases de datos vectoriales que manejan conjuntos de datos grandes.

Los administradores de bases de datos a menudo eligen entre árboles B e indexación basada en hash según sus necesidades. Los árboles B destacan en bases de datos relacionales, administrando eficientemente datos ordenados y consultas de rango en espacios de baja dimensionalidad, y manteniendo el orden para operaciones tradicionales.

Sin embargo, en bases de datos vectoriales que manejan datos de alta dimensionalidad (como las utilizadas en IA y aprendizaje automático), los árboles B tienen dificultades debido a la maldición de la dimensionalidad. A medida que aumentan las dimensiones, los árboles B se vuelven menos efectivos porque los datos se distribuyen de manera más uniforme, lo que dificulta la partición. En estos casos, la indexación basada en hash ofrece una alternativa convincente, que discutiremos a continuación, y puede proporcionar un mejor rendimiento para conjuntos de datos de alta dimensionalidad.

Algoritmo de indexación de hash

La indexación de hash es una técnica diseñada para mejorar la eficiencia de búsqueda, especialmente en contextos de alta dimensionalidad como bases de datos vectoriales. Opera de manera diferente a los árboles B y es particularmente útil para administrar conjuntos de datos grandes y complejos.

Cómo funciona la indexación de hash

La indexación de hash utiliza una función de hash (opens new window) para asignar claves a ubicaciones específicas en una tabla hash, lo que permite una recuperación eficiente de datos (opens new window). A diferencia de los árboles B, que mantienen una estructura equilibrada, los índices de hash proporcionan una complejidad temporal constante, O(1), para las operaciones de búsqueda, inserción y eliminación, lo que los hace ideales para consultas de coincidencia exacta. La función de hash convierte una clave en un código hash para determinar su índice en la tabla hash, mientras que los buckets almacenan las entradas en cada índice. Técnicas de manejo de colisiones, como el encadenamiento (listas enlazadas) o el direccionamiento abierto (sondeo), gestionan los casos en los que múltiples claves se asignan al mismo índice.

En bases de datos vectoriales, la indexación de hash se adapta para datos de alta dimensionalidad. Múltiples funciones de hash distribuyen vectores en varios buckets de hash. Durante una búsqueda del vecino más cercano, se recuperan vectores de los buckets relevantes y se comparan con el vector de consulta. La efectividad del método depende de la calidad de las funciones de hash y de cómo distribuyen los vectores en los buckets. La indexación de hash mejora la eficiencia de búsqueda para coincidencias exactas, pero es menos adecuada para consultas de rango o recuperación de datos ordenados.

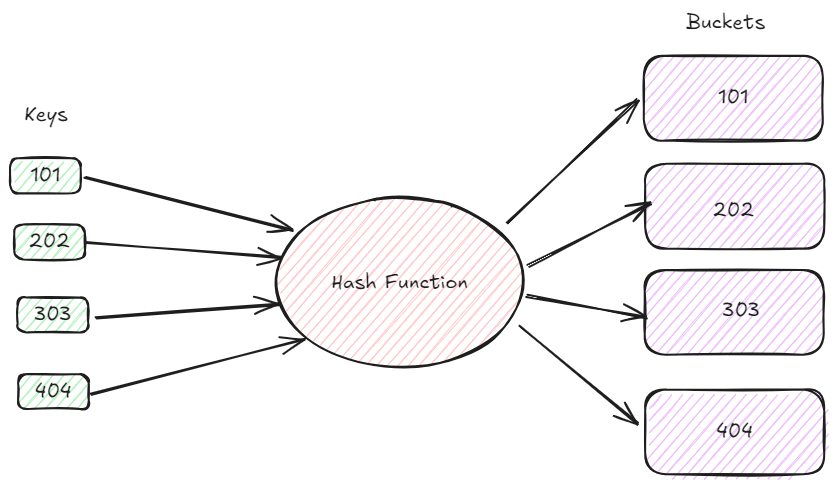
Ahora, para mejorar la comprensión, tomemos un ejemplo de una base de datos de una biblioteca donde necesitamos buscar eficientemente registros de libros por sus ID únicos. Supongamos que tenemos los siguientes ID de libros para indexar: 101, 202, 303 y 404.

Este diagrama muestra la idea fundamental de la indexación de hash. Comenzamos con una colección de ID de libros, que sirven como nuestras claves. Las claves pasan por una función de hash que las convierte en valores numéricos. Estos valores hash, etiquetados como tales, deciden el contenedor donde se colocarán los datos de libros relacionados. Idealmente, la función de hash distribuye uniformemente las claves entre los buckets para reducir las colisiones. En este caso, cada ID de libro está vinculado a un bucket distinto, mostrando una distribución de hash impecable. En situaciones reales, las colisiones son frecuentes y requieren métodos adicionales como el encadenamiento o el direccionamiento abierto para gestionarlas con éxito.

Ventajas de la indexación de hash

1. Búsqueda rápida: La indexación de hash proporciona una complejidad temporal constante en el caso promedio O(1) para las operaciones de búsqueda, lo que la hace extremadamente eficiente para consultas de coincidencia exacta.
2. Estructura simple: La estructura de tabla hash es sencilla, lo que simplifica la implementación y gestión en comparación con estructuras más complejas como los árboles B.
3. Eficiente para consultas puntuales: La indexación de hash destaca en escenarios donde las consultas se basan en coincidencias exactas, como recuperar un registro por un identificador único.

Limitaciones de la indexación de hash

1. Ineficiente para consultas de rango: La indexación de hash no es adecuada para consultas de rango o acceso ordenado a datos porque la función de hash no conserva el orden de las claves.
2. Overhead en el manejo de colisiones: El manejo de colisiones puede agregar overhead, especialmente si la tabla hash no tiene un tamaño adecuado o si las colisiones son frecuentes.
3. Tabla de tamaño fijo: Las tablas hash a menudo tienen un tamaño fijo y cambiar su tamaño puede ser complejo y costoso. Esto puede llevar a una degradación del rendimiento si la tabla se sobrecarga.
4. Falta de flexibilidad: A diferencia de los árboles B, los índices de hash no admiten consultas de rango eficientes o recorridos ordenados, lo que puede ser una desventaja significativa para aplicaciones que requieren tales operaciones.

Si bien la indexación de hash es excelente para consultas rápidas de coincidencia exacta, puede tener dificultades con datos de alta dimensionalidad. Para búsquedas aproximadas eficientes del vecino más cercano, la indexación de gráficos utilizando el algoritmo HNSW (Hierarchical Navigable Small World) ofrece una alternativa poderosa, que gestiona hábilmente vectores complejos y de alta dimensionalidad.

Boost Your AI App Efficiency now

Sign up for free to benefit from 150+ QPS with 5,000,000 vectors

Free Trial

Explore our product

Indexación de gráficos

La indexación de gráficos (opens new window) es muy útil para manejar redes de datos o relaciones complejas, como conexiones sociales o sistemas de recomendación. La indexación de gráficos, a diferencia de las estructuras de datos lineales como los árboles B o las tablas hash, está diseñada específicamente para manejar y recuperar eficientemente datos de gráficos, donde las conexiones entre entidades tienen igual importancia que las propias entidades.

En las bases de datos vectoriales modernas, los métodos de indexación basados en grafos (opens new window) como HNSW (Hierarchical Navigable Small World) (opens new window) son ampliamente utilizados para búsquedas de vecinos más cercanos aproximados (ANN) (opens new window), especialmente en espacios de alta dimensión. Estas técnicas avanzadas están diseñadas para navegar eficientemente a través de grandes y complejos conjuntos de datos.

Cómo funciona la indexación de gráficos

La indexación de gráficos implica crear estructuras que ayuden a localizar rápidamente nodos (vértices) y aristas (conexiones) en función de consultas específicas. El proceso de indexación puede centrarse en diferentes aspectos del gráfico, como las etiquetas de los nodos, los tipos de aristas o los caminos más cortos entre nodos. Se han desarrollado varios métodos de indexación de gráficos para optimizar diferentes tipos de consultas:

1. Indexación de caminos: Este método indexa caminos específicos dentro del gráfico, lo que hace que sea más rápido recuperar patrones o caminos comunes entre nodos. Es particularmente útil para consultas que implican recorrer el gráfico para encontrar relaciones o conexiones.
2. Indexación de subgráficos: En este enfoque, se indexan subgráficos frecuentes (componentes más pequeños del gráfico general), lo que permite búsquedas eficientes cuando se buscan patrones o estructuras específicas dentro de un gráfico más grande.
3. Indexación de vecindarios: Este método se centra en indexar los vecinos inmediatos de cada nodo, lo cual es útil para consultas que necesitan explorar conexiones o relaciones directamente vinculadas a un nodo específico.

HNSW (Hierarchical Navigable Small World)

HNSW es un algoritmo basado en gráficos que se crea específicamente para encontrar eficientemente los vecinos más cercanos en espacios vectoriales de alta dimensionalidad. El concepto principal de HNSW implica construir múltiples capas jerárquicas, donde cada capa es un gráfico que vincula nodos (puntos de datos) en función de su cercanía. Las capas superiores brindan un resumen general, mientras que las capas inferiores presentan información más detallada.

En la práctica, al realizar una búsqueda utilizando HNSW, el algoritmo comienza en la capa superior y navega a través del gráfico, descendiendo gradualmente a capas inferiores donde la búsqueda se vuelve más precisa. Este enfoque jerárquico reduce significativamente el espacio de búsqueda, lo que permite recuperar rápidamente los vecinos más cercanos, incluso en conjuntos de datos muy grandes.

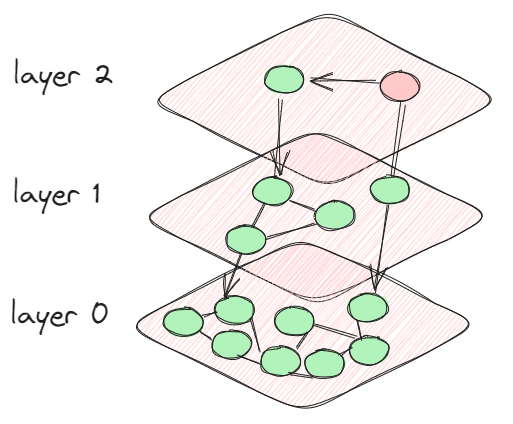
Imagina que estás buscando imágenes similares en una gran base de datos de datos visuales. Cada imagen está representada por un vector de alta dimensionalidad (por ejemplo, características extraídas de una red neuronal). HNSW te permite encontrar rápidamente las imágenes que son más cercanas a una imagen de consulta dada al recorrer el gráfico jerárquico, comenzando con una búsqueda amplia en las capas superiores y acercándose gradualmente a las coincidencias más cercanas en las capas inferiores. Los algoritmos de indexación de gráficos como HNSW están diseñados para minimizar el costo computacional asociado con tales recorridos, especialmente en gráficos grandes donde pueden existir millones de nodos y aristas. El proceso de indexación mejora significativamente el rendimiento de las consultas al centrarse en partes relevantes del gráfico.

Ventajas de la indexación de gráficos con HNSW

1. Optimizado para relaciones complejas: La indexación de gráficos destaca en la gestión y consulta de datos con relaciones complejas, como redes sociales, donde las conexiones entre entidades son cruciales.
2. Recorrido eficiente para búsquedas ANN: HNSW es altamente eficiente para realizar búsquedas aproximadas del vecino más cercano, que son cruciales para tareas como la recuperación de imágenes, sistemas de recomendación y otras aplicaciones que involucran datos de alta dimensionalidad.
3. Escalabilidad: HNSW se escala bien con conjuntos de datos grandes, maneja millones de vectores con una latencia relativamente baja.
4. Flexibilidad: HNSW se puede adaptar a varios casos de uso y ofrece un equilibrio entre precisión de búsqueda y eficiencia computacional.

Limitaciones de la indexación de gráficos con HNSW

1. Resultados aproximados: HNSW está diseñado para búsquedas aproximadas del vecino más cercano, lo que significa que no siempre devuelve la coincidencia más cercana exacta, aunque generalmente ofrece un buen equilibrio entre velocidad y precisión.
2. Implementación compleja: La indexación de gráficos, incluido HNSW, es más compleja de implementar en comparación con métodos de indexación tradicionales como los árboles B o la indexación de hash. Requiere algoritmos especializados adaptados a tipos específicos de consultas y estructuras de gráficos.
3. Intensivo en recursos: Debido a la complejidad de los datos de gráficos, la indexación y la consulta pueden ser intensivas en recursos, requiriendo más memoria y capacidad de procesamiento.
4. Uso de memoria: La estructura de gráfico multicapa de HNSW puede consumir una cantidad significativa de memoria, lo que podría ser una consideración en entornos con recursos limitados.

Si bien los árboles B y la indexación de hash funcionan bien para ciertos tipos de consultas, tienen dificultades con datos complejos o de alta dimensionalidad. Los métodos de indexación de gráficos como HNSW manejan estos desafíos al navegar eficientemente conexiones complejas. El Multi-Scale Tree Graph (MSTG) de MyScale (opens new window) lleva esto un paso más allá al combinar lo mejor de SQL y técnicas basadas en gráficos. MSTG utiliza una combinación de estructuras de árbol jerárquico y recorrido de gráficos para buscar rápidamente y con precisión en conjuntos de datos grandes y complejos. Esta combinación lo convierte en una herramienta poderosa para manejar los vastos y complejos datos de hoy en día.

Multi-Scale Tree Graph (MSTG)

El algoritmo Multi-Scale Tree Graph (MSTG), desarrollado por MyScale (opens new window), es una técnica de indexación avanzada diseñada para superar las limitaciones de los algoritmos de búsqueda de vectores tradicionales como HNSW (Hierarchical Navigable Small World) (opens new window) y IVF (Inverted File Indexing) (opens new window). MSTG es particularmente adecuado para manejar datos vectoriales de gran escala y alta dimensionalidad, ofreciendo un rendimiento superior tanto para búsquedas estándar como filtradas.

Cómo funciona MSTG

MSTG combina las fortalezas del agrupamiento jerárquico de árboles y el recorrido de gráficos para crear un mecanismo de búsqueda sólido y eficiente. Así es como funciona:

1. Agrupamiento jerárquico de árboles: En la etapa inicial, MSTG utiliza un enfoque de agrupamiento basado en árboles para organizar los datos en grupos. Esta estructura jerárquica ayuda a reducir el espacio de búsqueda, lo que hace que el proceso de recuperación sea más rápido y eficiente.
2. Recorrido de gráficos: Una vez que los datos están organizados en grupos, MSTG aplica técnicas de recorrido de gráficos para navegar entre estos grupos. Esto permite la recuperación rápida y precisa de los vecinos más cercanos, incluso en espacios complejos y de alta dimensionalidad.
3. Enfoque híbrido: La naturaleza híbrida de MSTG le permite administrar eficientemente regiones densas y dispersas del espacio vectorial. Esta adaptabilidad es clave para su rendimiento, especialmente en conjuntos de datos grandes donde los algoritmos tradicionales podrían tener dificultades.

Superar las limitaciones de otros algoritmos

MSTG aborda varias limitaciones clave de los algoritmos de búsqueda de vectores existentes:

1. Limitaciones de HNSW: Si bien HNSW es efectivo para búsquedas no filtradas, su rendimiento disminuye significativamente para búsquedas filtradas, especialmente cuando la proporción de filtro es baja. MSTG supera esto al mantener una alta precisión y velocidad incluso bajo condiciones de filtro restrictivas, gracias a su enfoque combinado de árbol y gráfico.
2. Limitaciones de IVF: IVF y sus variantes pueden sufrir un aumento en el tamaño del índice y una reducción en la eficiencia a medida que los conjuntos de datos crecen. MSTG mitiga estos problemas al reducir el consumo de recursos y mantener tiempos de búsqueda rápidos, incluso con conjuntos de datos masivos.
3. Eficiencia de recursos: MSTG aprovecha soluciones de almacenamiento eficientes en memoria, como SSD NVMe, para reducir el consumo de recursos que generalmente afecta a IVF y HNSW, lo que lo hace rentable y escalable para aplicaciones a gran escala.

MyScale (opens new window) optimiza la búsqueda de vectores filtrados (opens new window) con el exclusivo algoritmo MSTG que proporciona un salto significativo en el rendimiento para tareas de búsqueda de vectores, especialmente en escenarios que involucran conjuntos de datos grandes y complejos. Su enfoque híbrido y diseño eficiente en el uso de recursos lo convierten en una herramienta poderosa para las bases de datos vectoriales modernas, asegurando capacidades de búsqueda rápidas, precisas y escalables.

Join Our Newsletter

Subscribe

Tomar la decisión correcta para tu base de datos

La elección de un algoritmo de indexación debe adaptarse a tus requisitos específicos, teniendo en cuenta el tipo de datos, la frecuencia de las consultas y las necesidades de rendimiento de tu base de datos. Por ejemplo, si tu base de datos realiza con frecuencia consultas de rango o requiere capacidades de ordenación eficientes, un índice de árbol B podría ser más apropiado debido a su estructura optimizada para tales operaciones. Por otro lado, si tu enfoque principal se centra en consultas de coincidencia exacta y búsquedas rápidas, un índice de hash podría ofrecer un rendimiento superior en esos escenarios.

En resumen, comprender las características distintivas de cada algoritmo de indexación es esencial para tomar una decisión informada que optimice el rendimiento de las consultas en función de los requisitos únicos de tu base de datos.