En la era digital moderna, las recomendaciones personalizadas son vitales para mejorar las interacciones de los usuarios. Por ejemplo, una aplicación de streaming de música utiliza tus hábitos de escucha para recomendarte nuevas canciones que se ajusten a tu gusto, género o estado de ánimo. Sin embargo, ¿cómo deciden estos sistemas qué canciones son las más adecuadas para ti?
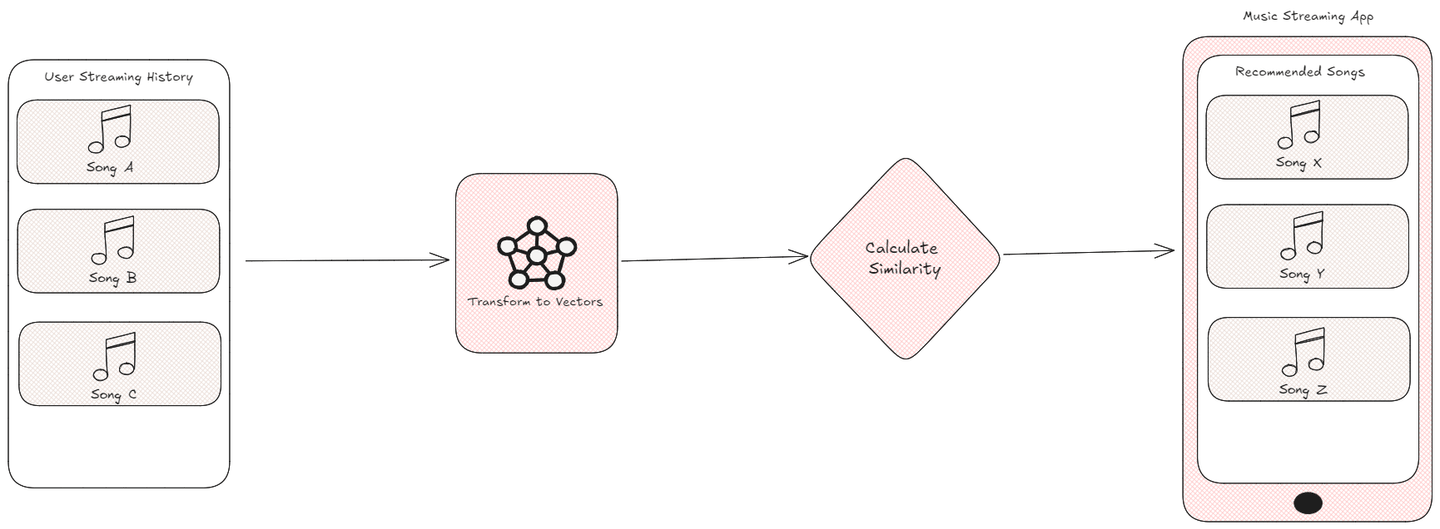
La respuesta radica en transformar estos puntos de datos en vectores y calcular su similitud utilizando métricas específicas. Al comparar los vectores que representan canciones, productos o comportamientos de los usuarios, los algoritmos pueden medir eficazmente sus características estrechamente relacionadas. Este proceso es fundamental en los campos del aprendizaje automático (opens new window) y la inteligencia artificial (opens new window), donde las métricas de similitud permiten a los sistemas ofrecer recomendaciones precisas, agrupar datos similares e identificar vecinos más cercanos, creando en última instancia una experiencia más personalizada y atractiva para los usuarios.
# ¿Qué son las Métricas de Similitud?
Las métricas de similitud son instrumentos utilizados para determinar el nivel de similitud o disimilitud entre dos entidades. Estos objetos pueden incluir documentos de texto, imágenes o puntos de datos dentro de un conjunto de datos. Considera las métricas de similitud como una herramienta para evaluar la cercanía de las relaciones entre elementos. Juegan un papel crucial en diversos sectores, como el aprendizaje automático, al ayudar a las computadoras a reconocer patrones en los datos, agrupar elementos similares y proporcionar sugerencias. Por ejemplo, al intentar descubrir películas similares a una que te gusta, las medidas de similitud ayudan a determinarlo examinando las características de diversas películas.
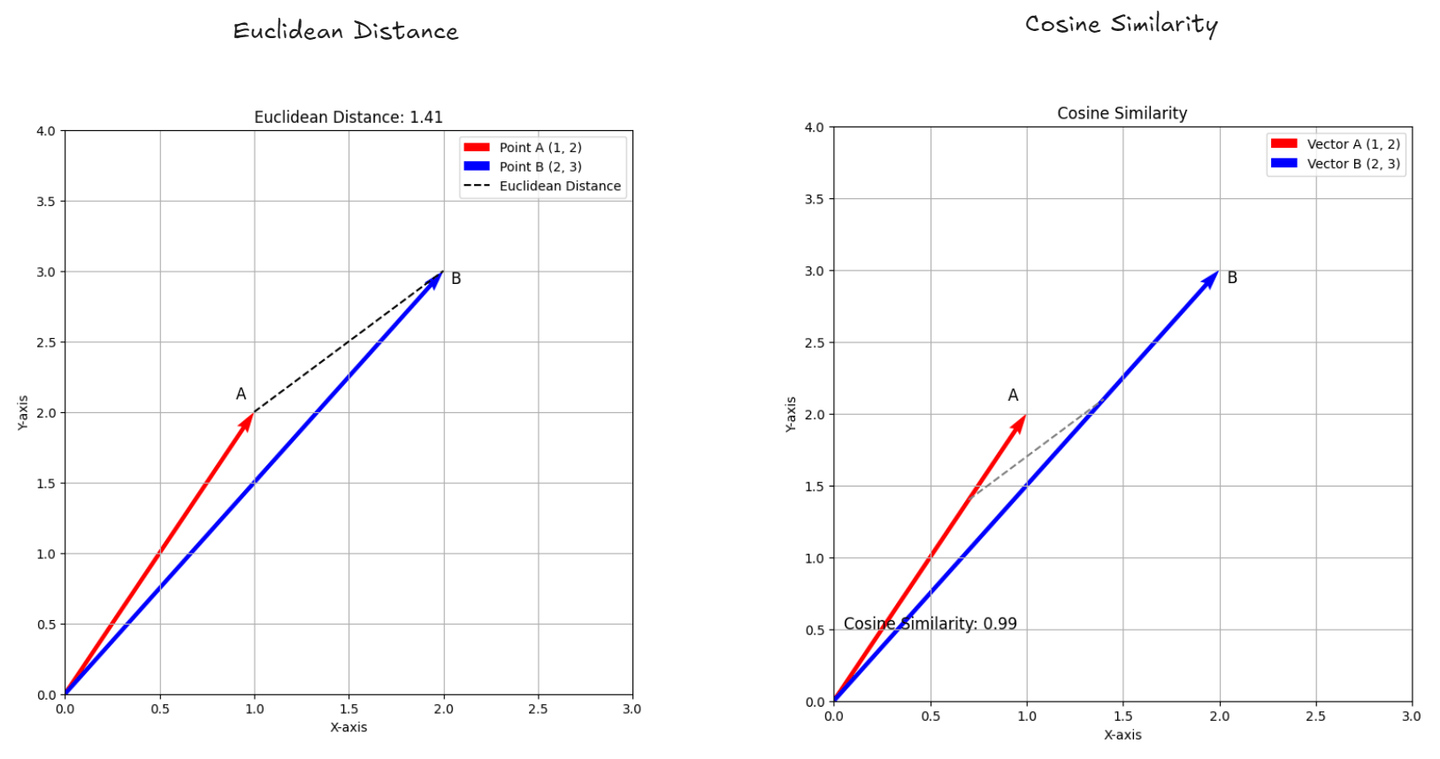
- Distancia Euclidiana: (opens new window) Mide qué tan lejos están dos puntos en el espacio, como medir la línea recta entre dos ubicaciones en un mapa. Te indica la distancia exacta entre ellos.
- Similitud del Coseno: (opens new window) Verifica qué tan similares son dos listas de números (como puntajes o características) al observar el ángulo entre ellas. Si el ángulo es pequeño, significa que las listas son muy similares, incluso si tienen longitudes diferentes. Te ayuda a comprender qué tan estrechamente relacionadas están dos cosas según su dirección.
Ahora exploremos ambos en detalle para comprender cómo funcionan.
# Distancia Euclidiana
La Distancia Euclidiana cuantifica la distancia entre dos puntos en un espacio multidimensional, midiendo su separación y revelando la similitud basada en la distancia espacial. Esta medida es especialmente valiosa en plataformas de compras en línea que sugieren productos a los clientes en función de sus hábitos de navegación y compra. Cada producto puede representarse como un punto en un espacio multidimensional, donde diferentes dimensiones representan aspectos como el precio, la categoría y las calificaciones de los usuarios.
El sistema calcula la Distancia Euclidiana entre los vectores de productos cuando un usuario ve o compra artículos específicos. Cuando dos productos están más cerca en distancia, se considera que son más similares, lo que ayuda al sistema a sugerir artículos que se ajusten a las preferencias del usuario.
# Fórmula:
La Distancia Euclidiana d entre dos puntos A(x1,y1) y B(x2,y2) en un espacio bidimensional se calcula mediante:
Para un espacio n-dimensional, la fórmula se generaliza a:
La fórmula calcula la distancia tomando la raíz cuadrada de la suma de las diferencias al cuadrado entre cada dimensión correspondiente de los dos puntos. Esencialmente, mide qué tan lejos están los dos puntos en línea recta, lo que lo convierte en una forma sencilla de evaluar la similitud.
# Ejemplo de código
Ahora codifiquemos un ejemplo que genere un gráfico para calcular la Distancia Euclidiana:
import numpy as np
import matplotlib.pyplot as plt
# Define dos puntos en un espacio 2D
punto_A = np.array([1, 2])
punto_B = np.array([2, 3])
# Calcula la Distancia Euclidiana
distancia_euclidiana = np.linalg.norm(punto_A - punto_B)
# Crea una figura y un eje
fig, ax = plt.subplots(figsize=(8, 8))
# Dibuja los puntos
ax.quiver(0, 0, punto_A[0], punto_A[1], angles='xy', scale_units='xy', scale=1, color='r', label='Punto A (1, 2)')
ax.quiver(0, 0, punto_B[0], punto_B[1], angles='xy', scale_units='xy', scale=1, color='b', label='Punto B (2, 3)')
# Establece los límites del gráfico
ax.set_xlim(0, 3)
ax.set_ylim(0, 4)
# Agrega una cuadrícula
ax.grid()
# Agrega etiquetas
ax.annotate('A', punto_A, textcoords="offset points", xytext=(-10,10), ha='center', fontsize=12)
ax.annotate('B', punto_B, textcoords="offset points", xytext=(10,-10), ha='center', fontsize=12)
# Dibuja una línea que representa la Distancia Euclidiana
ax.plot([punto_A[0], punto_B[0]], [punto_A[1], punto_B[1]], 'k--', label='Distancia Euclidiana')
# Agrega una leyenda
ax.legend()
# Agrega título y etiquetas
ax.set_title(f'Distancia Euclidiana: {distancia_euclidiana:.2f}')
ax.set_xlabel('Eje X')
ax.set_ylabel('Eje Y')
# Muestra el gráfico
plt.show()
Al ejecutar este código, se generará la siguiente salida.
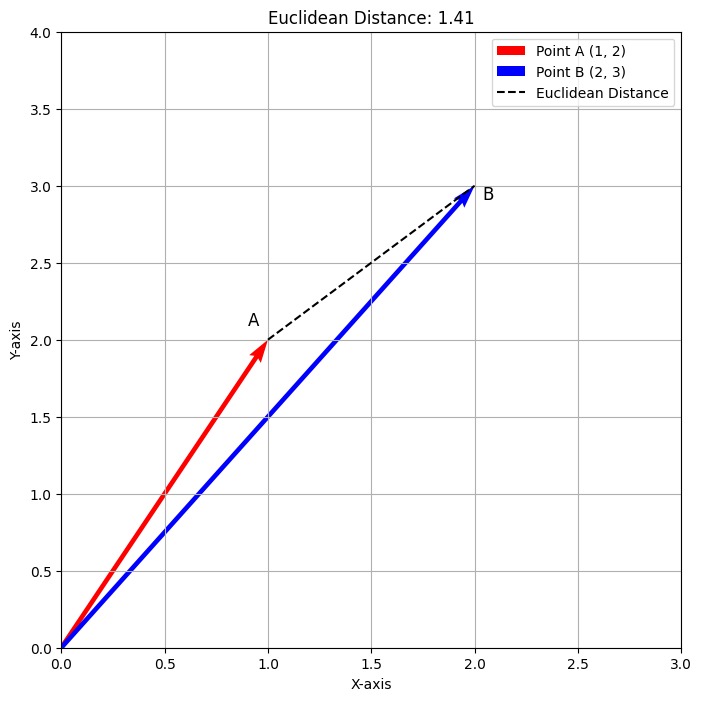
El gráfico anterior ilustra la Distancia Euclidiana entre los puntos A(1,2) y B(2,3). El vector rojo representa el Punto A, el vector azul representa el Punto B y la línea punteada indica la distancia, aproximadamente 1.41. Esta visualización proporciona una representación clara de cómo la Distancia Euclidiana mide el camino directo entre los dos puntos.
# Similitud del Coseno
La Similitud del Coseno es una métrica utilizada para medir qué tan similares son dos vectores, independientemente de su magnitud. Cuantifica el coseno del ángulo entre dos vectores no nulos en un espacio n-dimensional, proporcionando información sobre su similitud direccional. Esta medida es particularmente útil en sistemas de recomendación, como los utilizados por plataformas de contenido como Netflix o Spotify, donde ayuda a sugerir películas o canciones según las preferencias del usuario. En este contexto, cada elemento (por ejemplo, película o canción) puede representarse como un vector de características, como género, calificaciones e interacciones de los usuarios.
Cuando un usuario interactúa con elementos específicos, el sistema calcula la Similitud del Coseno entre los vectores correspondientes de los elementos. Si el valor del coseno es cercano a 1, indica un alto grado de similitud, lo que ayuda a la plataforma a recomendar elementos que se ajusten a los intereses del usuario.
# Fórmula:
La Similitud del Coseno S entre dos vectores A y B se calcula de la siguiente manera:
Donde:
- A⋅B es el producto escalar de los vectores.
- ∥A∥ y ∥B∥ son las magnitudes (o normas) de los vectores.
Esta fórmula calcula el coseno del ángulo entre los dos vectores, midiendo efectivamente su similitud basada en la dirección en lugar de la magnitud.
# Ejemplo de código
Ahora codifiquemos un ejemplo que calcule la Similitud del Coseno y visualice los vectores:
import numpy as np
import matplotlib.pyplot as plt
# Define dos vectores en un espacio 2D
vector_A = np.array([1, 2])
vector_B = np.array([2, 3])
# Calcula la Similitud del Coseno
producto_punto = np.dot(vector_A, vector_B)
norma_A = np.linalg.norm(vector_A)
norma_B = np.linalg.norm(vector_B)
similitud_coseno = producto_punto / (norma_A * norma_B)
# Crea una figura y un eje
fig, ax = plt.subplots(figsize=(8, 8))
# Dibuja los vectores
ax.quiver(0, 0, vector_A[0], vector_A[1], angles='xy', scale_units='xy', scale=1, color='r', label='Vector A (1, 2)')
ax.quiver(0, 0, vector_B[0], vector_B[1], angles='xy', scale_units='xy', scale=1, color='b', label='Vector B (2, 3)')
# Dibuja el ángulo entre los vectores
inicio_angulo = np.array([vector_A[0] * 0.7, vector_A[1] * 0.7])
fin_angulo = np.array([vector_B[0] * 0.7, vector_B[1] * 0.7])
ax.plot([inicio_angulo[0], fin_angulo[0]], [inicio_angulo[1], fin_angulo[1]], 'k--', color='gray')
# Anota el ángulo y la similitud del coseno
ax.text(0.5, 0.5, f'Similitud del Coseno: {similitud_coseno:.2f}', fontsize=12, color='black', ha='center')
# Establece los límites del gráfico
ax.set_xlim(0, 3)
ax.set_ylim(0, 4)
# Agrega una cuadrícula
ax.grid()
# Agrega anotaciones para los vectores
ax.annotate('A', vector_A, textcoords="offset points", xytext=(-10, 10), ha='center', fontsize=12)
ax.annotate('B', vector_B, textcoords="offset points", xytext=(10, -10), ha='center', fontsize=12)
# Agrega una leyenda
ax.legend()
# Agrega título y etiquetas
ax.set_title('Visualización de la Similitud del Coseno')
ax.set_xlabel('Eje X')
ax.set_ylabel('Eje Y')
# Muestra el gráfico
plt.show()
Al ejecutar este código, se generará la siguiente salida.
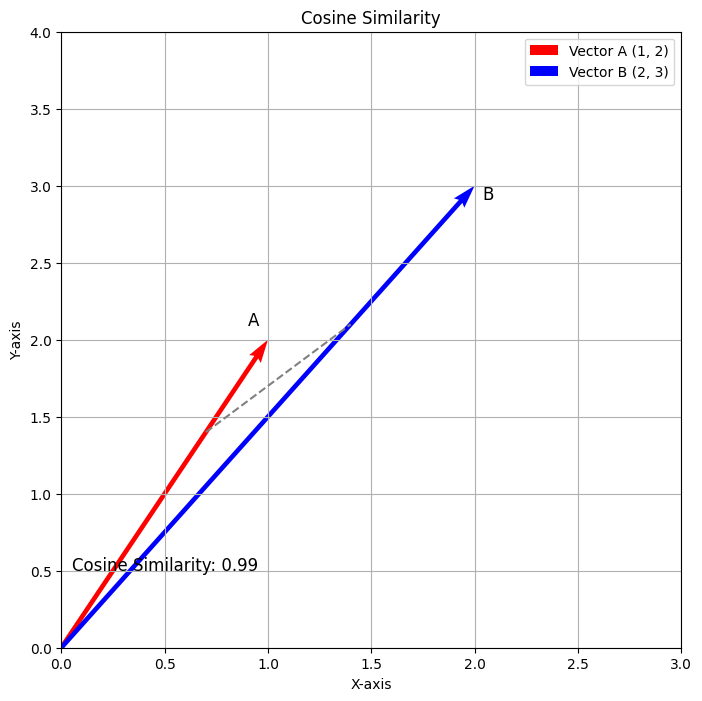
El gráfico anterior ilustra la Similitud del Coseno entre los vectores A(1,2) y B(2,3). El vector rojo representa el Vector A y el vector azul representa el Vector B. La línea punteada indica el ángulo entre los dos vectores, y la Similitud del Coseno calculada es aproximadamente 0.98. Esta visualización representa de manera efectiva cómo la Similitud del Coseno mide la relación direccional entre los dos vectores.
# Uso de Métricas de Similitud en Bases de Datos de Vectores
Las bases de datos de vectores desempeñan un papel crucial en los motores de recomendación y el análisis impulsado por IA al transformar datos no estructurados en vectores de alta dimensión para búsquedas de similitud eficientes. Las medidas cuantitativas como la Distancia Euclidiana y la Similitud del Coseno se utilizan para comparar estos vectores, lo que permite a los sistemas sugerir contenido adecuado o identificar irregularidades. Por ejemplo, los sistemas de recomendación combinan los gustos de los usuarios con los vectores de los elementos, ofreciendo recomendaciones personalizadas.
MyScale (opens new window) aprovecha estas métricas para potenciar su algoritmo MSTG (Multi-Scale Tree Graph) (opens new window), que combina estructuras basadas en árboles y gráficos para realizar búsquedas de vectores altamente eficientes, especialmente en conjuntos de datos grandes y filtrados. MSTG es particularmente efectivo en el manejo de búsquedas filtradas, superando a otros algoritmos como HNSW cuando los criterios de filtrado son estrictos, lo que permite búsquedas de vecinos más cercanos más rápidas y precisas.
El tipo de métrica en MyScale permite a los usuarios cambiar entre las métricas de distancia Euclidiana (L2), Coseno o Producto Interno (IP), según la naturaleza de los datos y el resultado deseado. Por ejemplo, en sistemas de recomendación o tareas de procesamiento del lenguaje natural, se utiliza con frecuencia la Similitud del Coseno para emparejar vectores, mientras que la Distancia Euclidiana es preferida para tareas que requieren proximidad espacial, como la detección de imágenes u objetos.
Al incorporar estas métricas en su algoritmo MSTG, MyScale optimiza las búsquedas de vectores en diversas modalidades de datos, lo que lo hace muy adecuado para aplicaciones que requieren análisis impulsado por IA rápido, preciso y escalable.
# Conclusión
En resumen, las medidas de similitud como la Distancia Euclidiana y la Similitud del Coseno desempeñan un papel crucial en el aprendizaje automático, los sistemas de recomendación y las aplicaciones de IA. Mediante la comparación de vectores que representan puntos de datos, estas métricas permiten a los sistemas descubrir conexiones entre objetos, lo que hace posible proporcionar sugerencias personalizadas o reconocer patrones en los datos. La Distancia Euclidiana calcula la distancia lineal entre puntos, mientras que la Similitud del Coseno examina la correlación direccional, y cada una tiene beneficios distintos según el escenario específico.
MyScale mejora la efectividad de estas métricas de similitud a través de su innovador algoritmo MSTG, que optimiza tanto la velocidad como la precisión de las búsquedas de similitud. Al integrar estructuras de árboles y gráficos, MSTG acelera el proceso de búsqueda, incluso con datos complejos y filtrados, lo que hace de MyScale una solución potente para análisis impulsado por IA de alto rendimiento, manejo de datos a gran escala y búsquedas de vectores precisas y eficientes.




