大規模な図書館に特定の本を探しに行くと想像してみてください。しかし、整理されたカタログがない場合、全ての棚を見る必要があり、それには数時間、あるいは数日かかるかもしれません。しかし、図書館が整理されたカタログを備えている場合、タイトル、著者、または主題の一覧を参照するだけで、必要な本を素早く見つけることができます。このような構造化されたアプローチにより、本を見つける速度と効率が向上します。
同様に、データベースでは、インデックスがその整理されたカタログの役割を果たします。インデックスは、データベースがデータを迅速に見つけて取得できるようにするシステムを作成することで、クエリのパフォーマンス (opens new window)を向上させます。カタログが本を素早く見つけるのを助けるように、インデックスはデータベースが必要なデータをより速く見つけるのを助けます。これを実現するために、データベースは異なるインデックスアルゴリズム (opens new window)を使用します。たとえば、ハッシュインデックスは、特定のデータを素早く見つけるために効果的であり、完全一致クエリ (opens new window)に適しています。別の方法であるB-ツリーインデックスは、検索を高速化するためにデータを構造化する方法です。
さらに、グラフインデックスは、ソーシャルネットワークの関係など、複雑な接続を持つデータの検索を最適化します。インデックスはデータベース内の道案内図のような役割を果たし、すべてのレコードをスキャンすることなく関連情報に迅速にアクセス (opens new window)できるようにします。これは、速度と正確性の両方が重要な大規模なデータセットを管理するために不可欠です。
# B-ツリーインデックスアルゴリズム
データベース管理において、B-ツリーインデックスアルゴリズムは、検索、挿入、削除の操作を最適化するために重要です。その設計と特性により、大規模なデータセットを効率的に管理するのに特に効果的です。
# B-ツリーインデックスの動作原理
B-ツリーは、ノードが複数の子を持つことを許可することでバランスを保ちます。これに対して、通常は2つの子ノードしか持たないバイナリサーチツリー (opens new window)とは異なります。この設計により、各ノードは複数のキーと子ノードへのポインタを格納できるため、すべての葉ノードが同じ深さに保たれ、データへの効率的なアクセスが可能となります。
これらの特徴は、B-ツリーインデックスの主な特性に貢献しています。バランスの取れた構造により、B-ツリーは検索、挿入、削除の操作に対してO(log n)の時間計算量を保証します。各ノードはt-1から2t-1のキーとtから2tの子を保持できるため、柔軟なストレージを提供します。このバランスにより、ツリーの高さがキーの数に対して対数的に保たれるため、大規模なデータセットでも効率的な操作が可能となります。さらに、ノード内のソートされたキーは効率的な範囲クエリや順序付けられたトラバーサルを可能にし、ツリーのパフォーマンスをさらに向上させます。
例を使って理解しましょう。
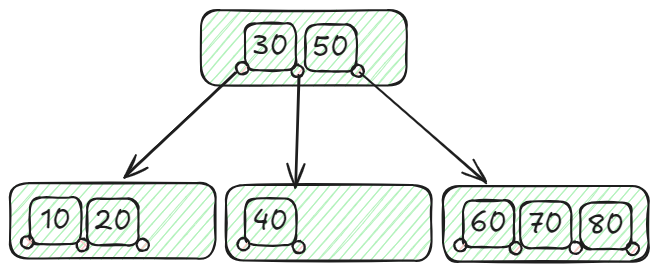
学生データベースを考えてみましょう。学生のIDで学生レコードを効率的に検索する必要があります。次の学生IDをインデックス化するとします:10、20、30、40、50、60、70、80。最小次数(t)が2のB-ツリーを構築します。
このB-ツリーでは、主ノードに2つのキー(30と50)があり、3つの子ノードがあります:30未満のID(10、20)を保持する左のノード、30から50までのID(40)を保持する中央のノード、50を超えるID(60、70、80)を保持する右のノード。この構造により、B-ツリーデータ構造を使用して学生のIDを効果的に処理して取得することができます。例えば、ID 40を見つけるためには、ルートから始めて、40が50と30の間にあることを確認します。したがって、40を含む中央の子ノードに進みます。このバランスの取れた構造により、時間計算量 (opens new window)がO(log n)の効率的な検索、挿入、削除機能が保証されます。
# B-ツリーインデックスの利点
B-ツリーインデックスは、順序付けられたデータを効率的かつ柔軟に管理するための柔軟性と効率性が高く評価されています。主な利点は次のとおりです:
- 効率的なフィルタリング検索: 特定の条件に基づいてノードを素早く絞り込む能力とバランスの取れたソートされた性質により、B-ツリーはフィルタリング検索に特に効果的です。この効率性により、複雑なフィルタを処理することで、大規模なデータセット全体で高いパフォーマンスを維持することができます。
- 一貫したパフォーマンス: B-ツリーのバランスの取れた性質により、検索、挿入、削除の操作は予測可能なパフォーマンスを持ちます。通常、時間計算量がO(log n)です。このバランスにより、データセットが成長しても効率が維持されます。
- 効率的な動的更新: B-ツリーは、頻繁な挿入と削除が発生するデータベースに適しています。バランスを保ち、検索パスを最適化する能力により、データ構造が常に変化する動的な環境に適応することができます。
- 効果的な範囲クエリ: B-ツリー内のソートされたキーは、効率的な範囲クエリや順序付けられたトラバーサルをサポートします。これは、特定の範囲やシーケンス内のデータにアクセスする操作に特に有用です。
- 最適化されたディスク使用: B-ツリーは、ノードごとに複数のキーとポインタを格納することで、検索操作に必要なディスクアクセスの回数を減らします。この設計により、ディスクI/O操作が最小限に抑えられ、大規模なデータセットのパフォーマンスが向上します。
# B-ツリーインデックスの制限
強みにもかかわらず、B-ツリーインデックスはすべてのシナリオで常に最適な選択肢ではありません。以下の制限を考慮してください:
- 高次元データのスケーラビリティの問題: ベクトルの次元数が増加すると、B-ツリーのパフォーマンスが低下することがあります。これは、データがより均一に広がるため、パーティショニングが困難になるため、高次元のデータが多く存在するデータベースには適していません。
- 静的な環境でのオーバーヘッド: 主に静的または読み取り専用のデータセットの場合、B-ツリーのバランスを維持するためのオーバーヘッドがパフォーマンスの利点を上回る場合があります。そのような場合は、より単純なインデックスメソッドの方が効率的かもしれません。
- 複雑さとメモリ使用量: B-ツリーを実装および管理することは、より単純なデータ構造と比較して複雑な場合があります。また、ノードごとに複数のキーとポインタを格納する必要があるため、メモリ使用量が増加する可能性があります。これは、メモリ制約のある環境で考慮する必要があります。
- メモリ使用量の増加: B-ツリーでは、ノードごとに複数のキーとポインタを格納する必要があるため、メモリ使用量が増加する可能性があります。これは、大規模なデータセットを扱うベクトルデータベースで懸念されることです。
データベース管理者は、B-ツリーとハッシュベースのインデックスから選択することが一般的です。B-ツリーは、関係データベースでの順序付けられたデータと範囲クエリの効率的な管理、および伝統的な操作のための順序の維持に優れています。
しかし、AIや機械学習で使用されるような高次元データを扱うベクトルデータベースでは、B-ツリーは次元の呪いのために苦労します。次元が増えると、データがより均一に広がり、パーティショニングが困難になるためです。このような場合、ハッシュベースのインデックスは魅力的な代替手段を提供し、高次元データセットに対してより優れたパフォーマンスを提供する可能性があります。
# ハッシュインデックスアルゴリズム
ハッシュインデックスは、特にベクトルデータベースなどの高次元のコンテキストで検索効率を向上させるために設計された技術です。B-ツリーやハッシュテーブルなどの従来のインデックスとは異なる方法で動作し、大規模で複雑なデータセットの管理に特に役立ちます。
# ハッシュインデックスの動作原理
ハッシュインデックスは、ハッシュ関数を使用してキーをハッシュテーブル内の特定の位置にマッピングし、効率的なデータの取得 (opens new window)を可能にします。B-ツリーとは異なり、バランスの取れた構造を維持しないハッシュインデックスは、検索、挿入、削除の操作に対して一定の時間計算量O(1)を提供し、完全一致クエリに適しています。ハッシュ関数は、キーをハッシュコードに変換してハッシュテーブル内のインデックスを決定し、バケツは各インデックスにエントリを格納します。複数のキーが同じインデックスにハッシュされる場合、チェイニング(リンクリスト)やオープンアドレッシング(プロービング)などの衝突処理技術が複数のキーを管理します。
ハッシュインデックスは、高次元データに適応されたハッシュ関数を使用します。複数のハッシュ関数は、ベクトルをさまざまなハッシュバケットに分散させます。最近傍探索では、関連するバケットからベクトルを取得し、クエリベクトルと比較します。この手法の効果は、ハッシュ関数の品質とベクトルがバケットに均等に分散するかどうかに依存します。ハッシュインデックスは、完全一致クエリの検索効率を向上させますが、範囲クエリや順序付けられたデータの取得には適していません。
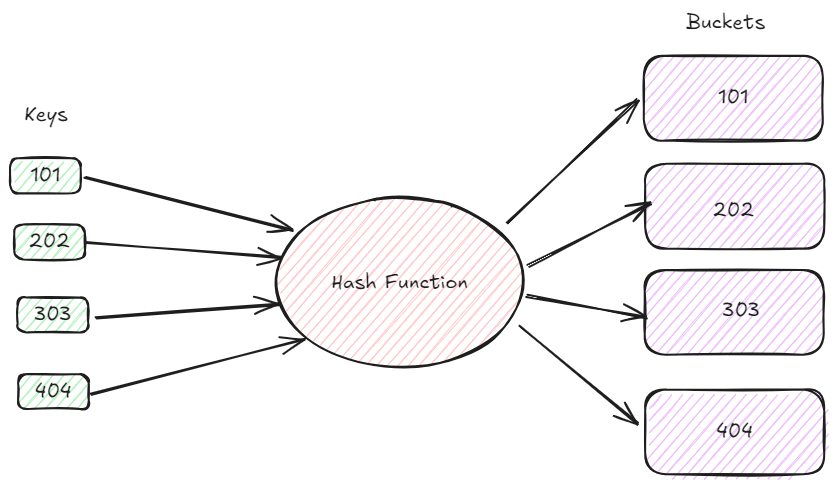
次に、図書館のデータベースを例にして、一意のIDによって本のレコードを効率的に検索する必要があるとします。次の本のIDをインデックス化するとします:101、202、303、404。
この図は、ハッシュインデックスの基本的なアイデアを示しています。キーとして機能する本のIDのコレクションから始めます。キーはハッシュ関数を通じて数値に変換されます。これらのハッシュ値は、関連する本のデータが配置されるコンテナを決定します。理想的には、ハッシュ関数はキーをバケット間に均等に分散させ、衝突を減らします。この例では、すべての本のIDが異なるバケットに関連付けられており、完璧なハッシュ分布が示されています。実際の状況では、衝突が頻繁に発生し、チェイニングやオープンアドレッシングなどの追加の方法が必要です。
# ハッシュインデックスの利点
- 高速な検索: ハッシュインデックスは、平均ケースで検索操作の時間計算量がO(1)であるため、完全一致クエリに対して非常に効率的です。
- シンプルな構造: ハッシュテーブルの構造はシンプルであり、B-ツリーやその他の複雑な構造と比較して実装と管理が容易です。
- ポイントクエリに効率的: ハッシュインデックスは、一意の識別子によるレコードの検索など、完全一致クエリに基づくシナリオで優れたパフォーマンスを発揮します。
# ハッシュインデックスの制限
- 範囲クエリに非効率: ハッシュインデックスは、範囲クエリや順序付けられたデータのアクセスには適していません。ハッシュ関数はキーの順序を保持しないためです。
- 衝突処理のオーバーヘッド: 衝突の処理にはオーバーヘッドが発生する場合があります。特にハッシュテーブルのサイズが適切でない場合や、衝突が頻繁に発生する場合です。
- 固定サイズのテーブル: ハッシュテーブルは通常固定サイズであり、サイズ変更が複雑でコストがかかる場合があります。テーブルが過負荷になるとパフォーマンスが低下する可能性があります。
- 柔軟性の欠如: ハッシュインデックスは、B-ツリーとは異なり、範囲クエリや順序付けられたトラバーサルを効率的にサポートしません。これは、そのような操作が必要なアプリケーションにとって重要な欠点となります。
ハッシュインデックスは、高速な完全一致クエリには優れていますが、高次元データには苦労します。効率的な近似最近傍(ANN)検索には、HNSW(Hierarchical Navigable Small World)アルゴリズムを使用したグラフインデックスが強力な代替手段を提供し、複雑な高次元ベクトルを効果的に管理します。
# グラフインデックス
グラフインデックスは、ソーシャルネットワークの関係など、複雑なデータネットワークや関係を処理するのに非常に役立ちます。グラフインデックスは、B-ツリーやハッシュテーブルなどの線形データ構造とは異なり、エンティティ間の接続がエンティティ自体と同じくらい重要な場合に効果的にデータを処理および取得するために特別に設計されています。
現代のベクトルデータベースでは、特に高次元空間での近似最近傍(ANN) (opens new window)検索には、HNSW(Hierarchical Navigable Small World) (opens new window)などのグラフベースのインデックス (opens new window)手法が広く使用されています。これらの高度な技術は、大規模で複雑なデータセットを効率的に処理するために設計されています。
# グラフインデックスの動作原理
グラフインデックスでは、特定のクエリに基づいてノード(頂点)とエッジ(接続)を迅速に見つけるための構造を作成します。インデックス作成プロセスは、ノードのラベル、エッジのタイプ、またはノード間の最短パスなど、グラフのさまざまな側面に焦点を当てる場合があります。さまざまな種類のクエリを最適化するために、いくつかのグラフインデックス手法が開発されています。
- パスインデックス: この方法では、グラフ内の特定のパスをインデックス化し、一般的なパターンやノード間のパスを素早く取得できるようにします。グラフをトラバースして関係や接続を見つけるクエリに特に有用です。
- サブグラフインデックス: このアプローチでは、よく出現するサブグラフ(大きなグラフの小さな構成要素)をインデックス化し、より大きなグラフ内の特定のパターンや構造を効率的に検索できるようにします。
- 近傍インデックス: この方法では、各ノードの直接の隣接ノードをインデックス化します。これは、特定のノードに直接リンクされた接続や関係を探索する必要があるクエリに役立ちます。
# HNSW(Hierarchical Navigable Small World)
HNSWは、高次元ベクトル空間で最も近い隣人を効率的に見つけるために作成されたグラフに基づくアルゴリズムです。HNSWの主なコンセプトは、複数の階層を持つグラフを構築することで、ノード(データポイント)を近さに基づいてリンクすることです。上位の階層は一般的な概要を示し、下位の階層はより詳細な情報を提供します。
実際には、HNSWを使用して検索を実行すると、アルゴリズムはトップレベルから始まり、グラフをトラバースして徐々に下位の階層に移動します。下位の階層では、検索がより正確になります。この階層構造により、検索空間が大幅に削減され、非常に大きなデータセットでも最も近い隣人を迅速に取得することができます。
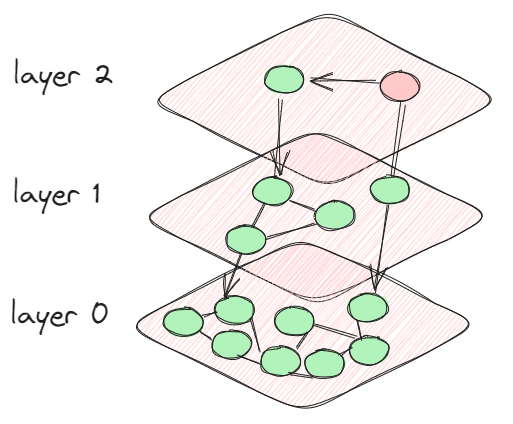
大規模なビジュアルデータベースで類似した画像を検索する場合を想像してみてください。各画像は高次元ベクトル(たとえば、ニューラルネットワークから抽出された特徴)で表されます。HNSWを使用すると、上位の階層から始めて、下位の階層に移動することで、階層的なグラフをトラバースすることで、与えられたクエリ画像に最も近い画像を素早く見つけることができます。
HNSWなどのグラフインデックスアルゴリズムは、特に数百万のノードとエッジが存在する大規模なグラフで、トラバースに関連する計算コストを最小限に抑えるように設計されています。インデックス作成プロセスにより、グラフの関連部分に焦点を当てることで、クエリのパフォーマンスが大幅に向上します。
# HNSWによるグラフインデックスの利点
- 複雑な関係に最適化: グラフインデックスは、関係データが複雑なデータやソーシャルネットワークなどのデータを管理およびクエリするのに優れています。エンティティ間の接続が重要な場合に効果的です。
- 近似最近傍(ANN)検索の効率的なトラバーサル: HNSWは、近似最近傍検索を効率的に実行するために非常に効率的です。これは、画像検索、レコメンデーションシステムなど、高次元データを含むタスクに重要です。
- スケーラビリティ: HNSWは大規模なデータセットでもスケーラブルであり、低レイテンシで数百万のベクトルを処理します。
- 柔軟性: HNSWはさまざまなユースケースに適応でき、検索の精度と計算効率のバランスを提供します。
# HNSWによるグラフインデックスの制限
- 近似結果: HNSWは近似最近傍検索のために設計されているため、常に最も近い一致を返すわけではありませんが、通常は速度と精度のトレードオフを提供します。
- 複雑な実装: グラフインデックス、HNSWを含むものは、B-ツリーやハッシュインデックスなどの従来のインデックス方法と比較して実装が複雑です。特定のクエリタイプとグラフ構造に合わせた専用のアルゴリズムが必要です。
- リソースの消費: グラフデータの複雑さにより、インデックス作成とクエリの処理がリソースを消費する場合があります。メモリと処理能力が必要です。
- メモリ使用量: HNSWの多層グラフ構造は、かなりのメモリを消費する場合があります。リソース制約のある環境では、これを考慮する必要があります。
B-ツリーやハッシュインデックスは特定のクエリタイプには適していますが、複雑なデータや高次元データには苦労します。HNSWなどのグラフインデックスは、複雑な接続を効率的にナビゲートすることでこれらの課題に対処します。MyScale (opens new window)の**Multi-Scale Tree Graph (MSTG)**は、SQLとグラフベースの技術のベストを組み合わせたもので、大規模で複雑なデータを迅速かつ正確に検索するための強力なツールです。この組み合わせにより、現代の広範で複雑なデータを扱うための高速かつスケーラブルな検索機能が実現されます。
# Multi-Scale Tree Graph (MSTG)
**Multi-Scale Tree Graph (MSTG)**アルゴリズムは、MyScale (opens new window)によって開発された高度なインデックス技術であり、HNSW(Hierarchical Navigable Small World) (opens new window)やIVF(Inverted File Indexing) (opens new window)などの従来のベクトル検索アルゴリズムの制限を克服するために設計されています。MSTGは、標準的な検索とフィルタリングされた検索の両方に優れたパフォーマンスを提供し、大規模で高次元のベクトルデータを効率的に処理します。
# MSTGの動作原理
MSTGは、階層的なツリークラスタリングとグラフトラバーサルの利点を組み合わせて、堅牢で効率的な検索メカニズムを作成します。以下にその動作原理を説明します。
- 階層的なツリークラスタリング: MSTGは、初期段階ではツリーベースのクラスタリング手法を使用してデータをクラスタに整理します。この階層構造により、検索空間が削減され、検索プロセスが迅速かつ効率的になります。
- グラフトラバーサル: データがクラスタに整理されると、MSTGはグラフトラバーサル技術を適用してこれらのクラスタ間を移動します。これにより、複雑な高次元空間でも最も近い隣人を迅速かつ正確に取得することができます。
- ハイブリッドアプローチ: MSTGのハイブリッドな性質により、ベクトル空間の密な領域と疎な領域の両方を効率的に管理できます。これは、従来のアルゴリズムが苦労する大規模なデータセットでのパフォーマンスに重要です。
# 他のアルゴリズムの制限の克服
MSTGは、既存のベクトル検索アルゴリズムのいくつかの主な制限に対処します。
- HNSWの制限: HNSWはフィルタリングされていない検索には効果的ですが、フィルタリングされた検索ではパフォーマンスが著しく低下します。特にフィルタ比率が低い場合には、MSTGはツリーとグラフベースのアプローチにより、制限の厳しいフィルタ条件下でも高い精度と速度を維持します。
- IVFの制限: IVFおよびその派生は、データセットが大きくなるにつれてインデックスのサイズが増加し、効率が低下する場合があります。MSTGはリソース消費を減らし、大規模なデータセットでも高速な検索時間を維持することで、これらの問題を緩和します。
- リソースの効率化: MSTGは、NVMe SSDなどのメモリ効率の高いストレージソリューションを活用して、通常IVFやHNSWに関連するリソース消費を減らし、コスト効果の高いスケーラビリティを実現します。
MyScale (opens new window)は、ユニークなMSTGアルゴリズムによるフィルタベクトル検索を最適化 (opens new window)し、大規模で複雑なデータに対するベクトル検索タスクのパフォーマンスを飛躍的に向上させます。そのハイブリッドアプローチとリソース効率の設計により、モダンなベクトルデータベースにおいて高速かつ正確なスケーラブルな検索機能が実現されます。
# データベースに適した選択肢をする
インデックスアルゴリズムの選択は、データベースのデータタイプ、クエリ頻度、およびパフォーマンスの要件に合わせてカスタマイズする必要があります。たとえば、データベースが頻繁に範囲クエリを実行したり、効率的なソート機能が必要な場合、B-ツリーインデックスはそのような操作に最適化された構造を持っているため、より適しているかもしれません。一方、完全一致クエリと高速なルックアップが主な焦点である場合、ハッシュインデックスがそれらのシナリオで優れたパフォーマンスを提供する可能性があります。
まとめると、各インデックスアルゴリズムの特徴を理解することは、データベースのユニークな要件に基づいてパフォーマンスを最適化するために重要です。




