現代のデジタル時代において、パーソナライズされた提案はユーザーとのインタラクションを向上させるために不可欠です。たとえば、音楽ストリーミングアプリケーションは、あなたの聴取習慣に基づいて、あなたの好み、ジャンル、または気分に合った新しい曲を推薦します。しかし、これらのシステムはどのようにして、どの曲があなたに最も適していると判断するのでしょうか?
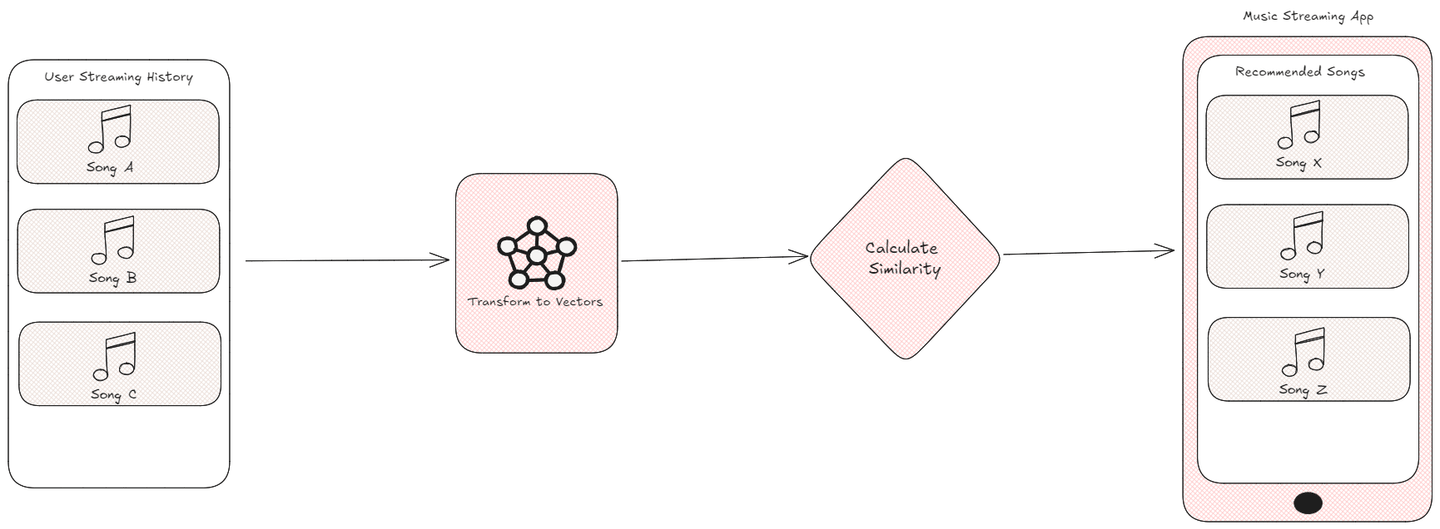
その答えは、これらのデータポイントをベクトルに変換し、特定の指標を使用してその類似性を計算することにあります。曲や製品、ユーザーの行動を表すベクトルを比較することで、アルゴリズムは効果的にそれらの関連する特徴を測定することができます。このプロセスは、機械学習 (opens new window)や人工知能 (opens new window)の分野で基本的なものであり、類似性の指標によってシステムは正確な推薦を行い、類似したデータをクラスタリングし、最も近い近傍を特定することができます。これにより、ユーザーによりパーソナライズされた魅力的な体験が提供されます。
# 類似性の指標とは?
類似性の指標は、2つのエンティティ間の類似性または非類似性のレベルを判断するために使用されるツールです。これらのオブジェクトには、テキストドキュメント、画像、またはデータセット内のデータポイントなどが含まれることがあります。類似性の指標は、アイテム間の関係の近さを評価するためのツールと考えることができます。これらは、機械学習などのさまざまなセクターで重要な役割を果たし、コンピュータがデータ内のパターンを認識し、類似したアイテムをクラスタリングし、提案を行うのに役立ちます。たとえば、好きな映画に似た映画を見つけようとする場合、類似性の測定はさまざまな映画の特徴を調べることでこれを判断するのに役立ちます。
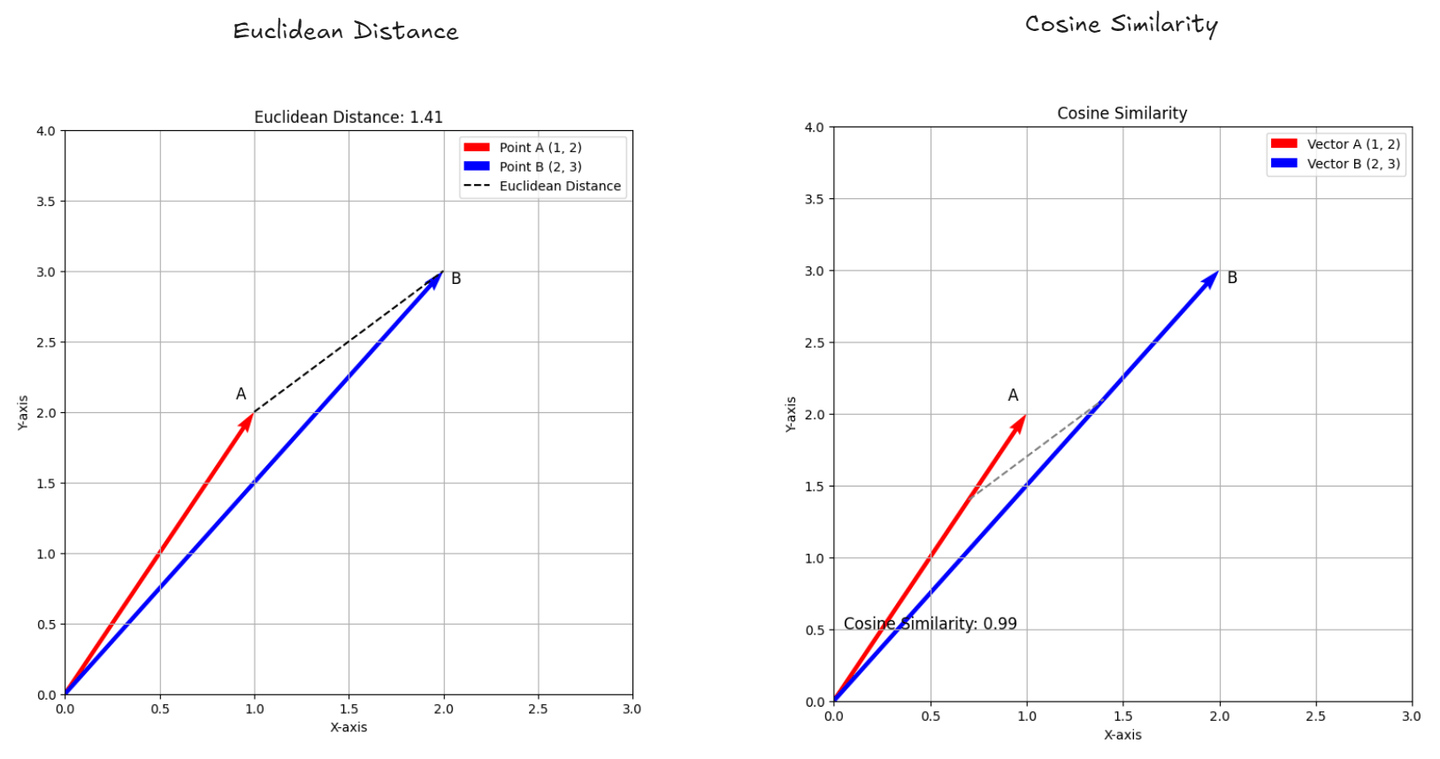
- ユークリッド距離: (opens new window) これは、2つの点が空間上でどれだけ離れているかを測定します。地図上の2つの場所間の直線距離を測定するのと同じです。それはそれらの間の正確な距離を示します。
- コサイン類似度: (opens new window) これは、2つの数値のリスト(スコアや特徴など)がどれだけ似ているかを、それらの間の角度を見ることで確認します。角度が小さいほど、リストは非常に似ていることを意味します。リストの長さが異なっていても、それらがどれだけ関連しているかを理解するのに役立ちます。
それでは、それぞれを詳しく見て、それらがどのように機能するかを理解しましょう。
# ユークリッド距離
ユークリッド距離は、多次元空間における2つの点の距離を定量化し、空間的な距離に基づいて類似性を明らかにします。この測定は、オンラインショッピングプラットフォームで特定の商品を顧客に提案する際に特に有用です。ここでは、価格、カテゴリ、ユーザーの評価などの側面を表す異なる次元が商品を多次元空間上の点として表現します。
ユーザーが特定の商品を見たり購入したりすると、システムは商品ベクトル間のユークリッド距離を計算します。距離が近いほど、より似ていると見なされ、システムはユーザーの好みに合った商品を提案するのに役立ちます。
# 公式:
2次元空間における2点A(x1,y1)とB(x2,y2)のユークリッド距離dは次のように与えられます:
n次元空間では、公式は次のように一般化されます:
この公式は、2つの点の対応する次元ごとの差の2乗の和の平方根を取ることで距離を計算します。基本的には、2つの点が直線上でどれだけ離れているかを測定し、類似性を評価するための直接的な方法です。
# コーディング例
それでは、ユークリッド距離を計算するためのグラフを生成する例のコードを書いてみましょう。
import numpy as np
import matplotlib.pyplot as plt
# 2次元空間の2つの点を定義する
point_A = np.array([1, 2])
point_B = np.array([2, 3])
# ユークリッド距離を計算する
euclidean_distance = np.linalg.norm(point_A - point_B)
# 図と軸を作成する
fig, ax = plt.subplots(figsize=(8, 8))
# 点をプロットする
ax.quiver(0, 0, point_A[0], point_A[1], angles='xy', scale_units='xy', scale=1, color='r', label='Point A (1, 2)')
ax.quiver(0, 0, point_B[0], point_B[1], angles='xy', scale_units='xy', scale=1, color='b', label='Point B (2, 3)')
# グラフの範囲を設定する
ax.set_xlim(0, 3)
ax.set_ylim(0, 4)
# グリッドを追加する
ax.grid()
# ラベルを追加する
ax.annotate('A', point_A, textcoords="offset points", xytext=(-10,10), ha='center', fontsize=12)
ax.annotate('B', point_B, textcoords="offset points", xytext=(10,-10), ha='center', fontsize=12)
# ユークリッド距離を表す線を描画する
ax.plot([point_A[0], point_B[0]], [point_A[1], point_B[1]], 'k--', label='Euclidean Distance')
# 凡例を追加する
ax.legend()
# タイトルとラベルを追加する
ax.set_title(f'Euclidean Distance: {euclidean_distance:.2f}')
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis')
# プロットを表示する
plt.show()
このコードを実行すると、以下の出力が生成されます。
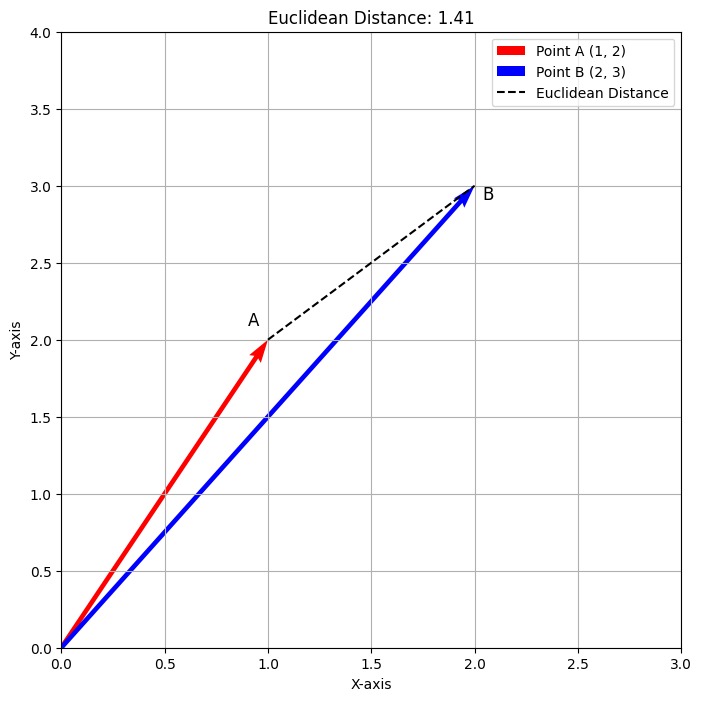
上記のプロットは、点A(1,2)と点B(2,3)のユークリッド距離を示しています。赤いベクトルは点Aを示し、青いベクトルは点Bを示しており、点Aと点Bの間の距離、およそ1.41を示す破線が描かれています。この可視化は、ユークリッド距離が2つの点の直接的な経路を測定する方法を明確に表しています。
# コサイン類似度
コサイン類似度は、2つのベクトルがどれだけ似ているかを測定するために使用される指標であり、それらの大きさに関係なく計測します。n次元空間のゼロでない2つのベクトルの間の角度のコサインを定量化し、それらの方向性の類似性についての洞察を提供します。この測定は、NetflixやSpotifyなどのコンテンツプラットフォームが使用する推薦システムなどの場面で特に有用です。ここでは、ジャンル、評価、ユーザーの相互作用などの特徴を持つベクトルとして各アイテム(映画や曲など)を表現することができます。
ユーザーが特定のアイテムと対話すると、システムは対応するアイテムベクトル間のコサイン類似度を計算します。コサインの値が1に近い場合、高い類似性を示し、プラットフォームはユーザーの興味に合ったアイテムを推薦するのに役立ちます。
# 公式:
2つのベクトルAとBのコサイン類似度Sは次のように計算されます:
ここで:
- A⋅Bはベクトルの内積です。
- ∥A∥ および ∥B∥はベクトルの大きさ(またはノルム)です。
この公式は、2つのベクトル間の角度のコサインを計算し、大きさではなく方向に基づいて類似性を測定します。
# コーディング例
それでは、コサイン類似度を計算し、ベクトルを可視化する例のコードを書いてみましょう。
import numpy as np
import matplotlib.pyplot as plt
# 2次元空間の2つのベクトルを定義する
vector_A = np.array([1, 2])
vector_B = np.array([2, 3])
# コサイン類似度を計算する
dot_product = np.dot(vector_A, vector_B)
norm_A = np.linalg.norm(vector_A)
norm_B = np.linalg.norm(vector_B)
cosine_similarity = dot_product / (norm_A * norm_B)
# 図と軸を作成する
fig, ax = plt.subplots(figsize=(8, 8))
# ベクトルをプロットする
ax.quiver(0, 0, vector_A[0], vector_A[1], angles='xy', scale_units='xy', scale=1, color='r', label='Vector A (1, 2)')
ax.quiver(0, 0, vector_B[0], vector_B[1], angles='xy', scale_units='xy', scale=1, color='b', label='Vector B (2, 3)')
# ベクトル間の角度を描画する
angle_start = np.array([vector_A[0] * 0.7, vector_A[1] * 0.7])
angle_end = np.array([vector_B[0] * 0.7, vector_B[1] * 0.7])
ax.plot([angle_start[0], angle_end[0]], [angle_start[1], angle_end[1]], 'k--', color='gray')
# 角度とコサイン類似度を注釈する
ax.text(0.5, 0.5, f'Cosine Similarity: {cosine_similarity:.2f}', fontsize=12, color='black', ha='center')
# グラフの範囲を設定する
ax.set_xlim(0, 3)
ax.set_ylim(0, 4)
# グリッドを追加する
ax.grid()
# ベクトルの注釈を追加する
ax.annotate('A', vector_A, textcoords="offset points", xytext=(-10, 10), ha='center', fontsize=12)
ax.annotate('B', vector_B, textcoords="offset points", xytext=(10, -10), ha='center', fontsize=12)
# 凡例を追加する
ax.legend()
# タイトルとラベルを追加する
ax.set_title('Cosine Similarity Visualization')
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis')
# プロットを表示する
plt.show()
このコードを実行すると、以下の出力が生成されます。
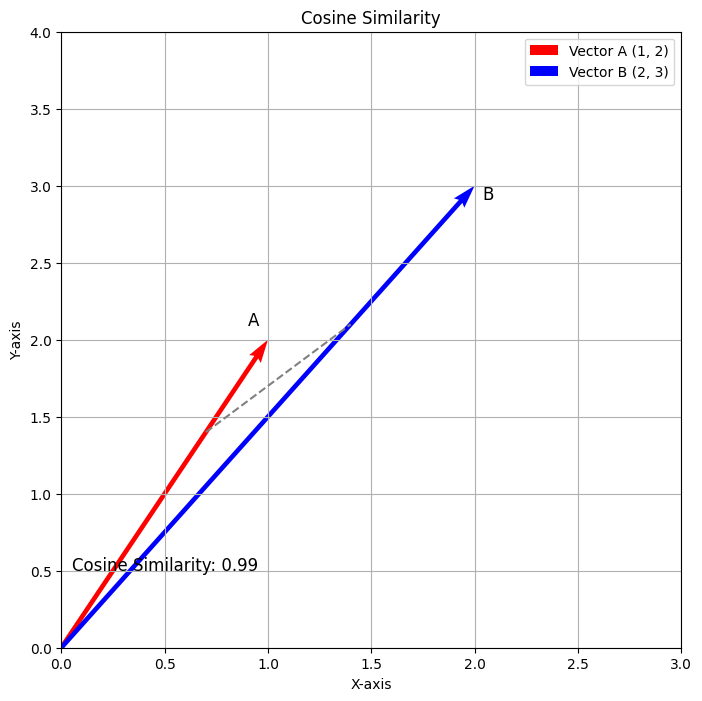
上記のプロットは、ベクトルA(1,2)とベクトルB(2,3)のコサイン類似度を示しています。赤いベクトルはベクトルAを示し、青いベクトルはベクトルBを示しています。破線は2つのベクトル間の角度を示し、計算されたコサイン類似度はおよそ0.98です。この可視化は、コサイン類似度が2つのベクトル間の方向関係を測定する方法を効果的に表しています。
# ベクトルデータベースでの類似性の指標の使用
ベクトルデータベースは、推薦エンジンやAI駆動の分析において、非構造化データを効率的な類似性検索のための高次元ベクトルに変換することで重要な役割を果たしています。ユークリッド距離やコサイン類似度などの定量的な指標を使用して、これらのベクトルを比較することで、システムは適切なコンテンツを推薦したり、異常を検出したりすることができます。たとえば、推薦システムはユーザーの好みとアイテムベクトルを組み合わせて、カスタマイズされた推薦を提供します。
MyScale (opens new window)は、その革新的なMSTG (Multi-Scale Tree Graph) (opens new window)アルゴリズムを活用して、ツリーとグラフベースの構造を組み合わせて、大規模なフィルタリングされたデータセットでも非常に効率的なベクトル検索を実行します。MSTGは、フィルタリングの基準が厳しい場合にHNSWなどの他のアルゴリズムよりも優れたパフォーマンスを発揮し、より迅速かつ正確な最近傍検索を可能にします。
MyScaleのメトリックタイプは、データの性質と望ましい結果に応じて、ユークリッド(L2)、コサイン、または**内積(IP)**の距離メトリックを切り替えることができます。たとえば、推薦システムやNLPのタスクでは、ベクトルのマッチングにコサイン類似度が頻繁に使用され、画像やオブジェクト検出などの空間的な近接性が必要なタスクではユークリッド距離が好まれます。
これらのメトリックをMSTGアルゴリズムに組み込むことで、MyScaleはさまざまなデータモダリティにわたるベクトル検索を最適化し、高速かつ正確なAI駆動の分析に非常に適しています。
# 結論
まとめると、ユークリッド距離やコサイン類似度などの類似性の測定は、機械学習、推薦システム、AIアプリケーションにおいて重要な役割を果たしています。データポイントを表すベクトルの比較を通じて、これらの指標はオブジェクト間の関連性を明らかにし、パーソナライズされた提案を提供したり、データ内のパターンを認識したりすることができます。ユークリッド距離は点間の直線距離を計算し、コサイン類似度は方向性の相関を調べることで、それぞれ特定のシナリオに基づいた異なる利点を持っています。
MyScaleは、その革新的なMSTGアルゴリズムによって、類似性の測定の効果を高めます。ツリーとグラフ構造を統合することで、MSTGは複雑なフィルタリングされたデータでも検索プロセスを高速化し、迅速かつ正確な最近傍検索を実現します。MyScaleは、高性能なAI駆動の分析、大規模なデータ処理、正確で効率的なベクトル検索が必要なアプリケーションに非常に適しています。




