在现代数字时代,个性化建议对于增强用户互动至关重要。例如,音乐流媒体应用程序利用您的听歌习惯来推荐与您的口味、流派或心情相符的新歌曲。然而,这些系统是如何决定哪些歌曲最适合您的呢?
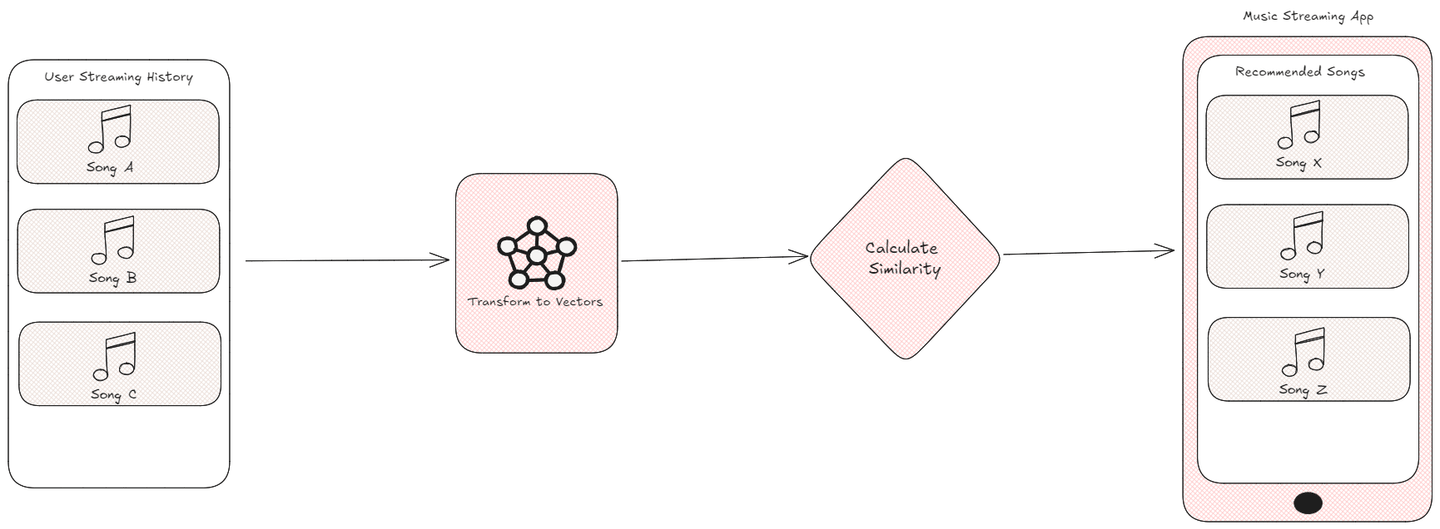
答案在于将这些数据点转化为向量,并使用特定的度量标准计算它们的相似性。通过比较表示歌曲、产品或用户行为的向量,算法可以有效地衡量它们之间的相关特征。这个过程在机器学习和人工智能领域中至关重要,其中相似性度量使系统能够提供准确的推荐、聚类相似数据并识别最近邻居,从而为用户创造更个性化和吸引人的体验。
# 什么是相似性度量?
相似性度量是用于确定两个实体之间相似性或不相似性水平的工具。这些对象可以包括文本文档、图像或数据集中的数据点。可以将相似性度量视为评估项目之间关系密切程度的工具。它们在机器学习等各个领域发挥着关键作用,帮助计算机识别数据中的模式、聚类相似项并提供建议。例如,当尝试发现与您喜欢的电影类似的电影时,相似性度量通过检查不同电影的特征来确定这一点。
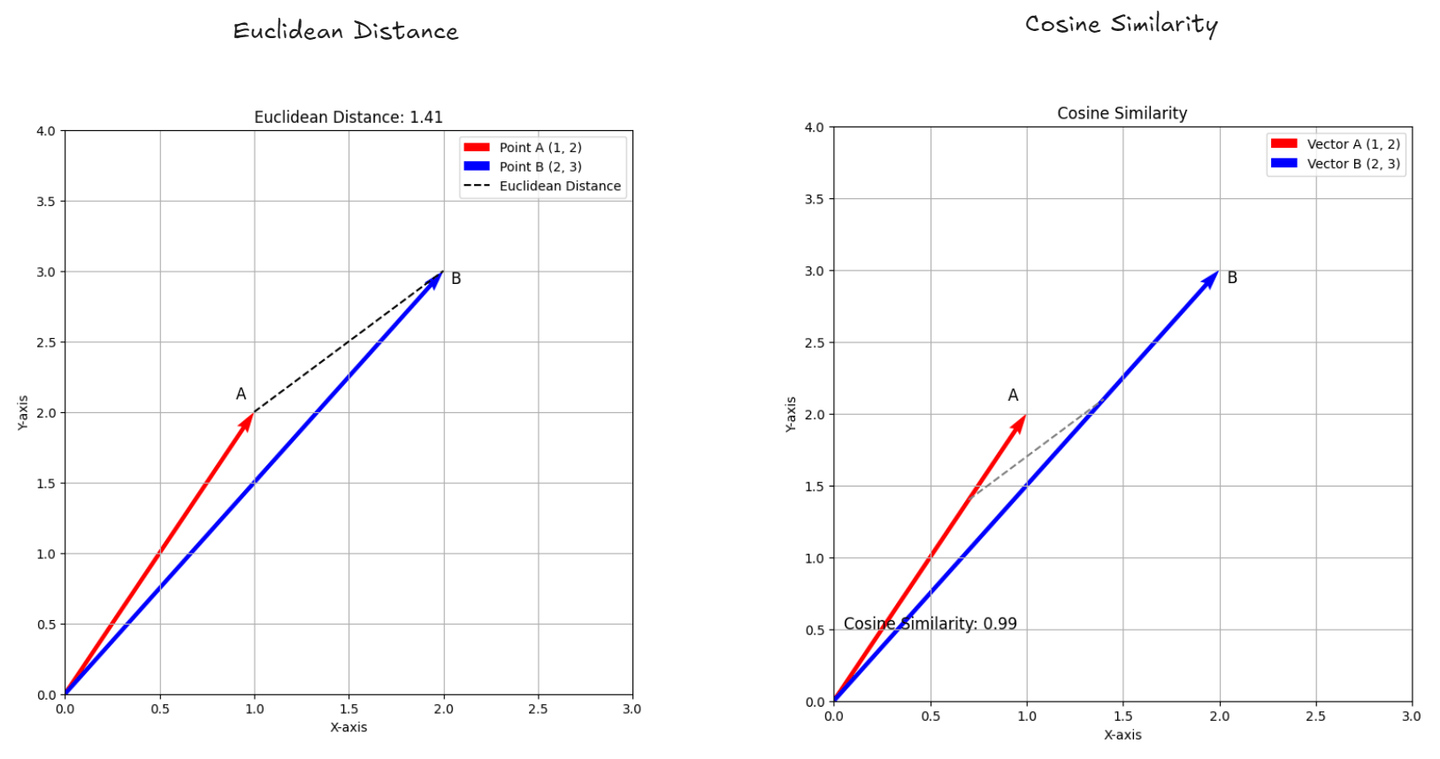
- 欧几里得距离: (opens new window)它衡量了空间中两点之间的距离,就像测量地图上两个位置之间的直线距离一样。它告诉您它们之间的确切距离。
- 余弦相似度: (opens new window)它通过查看两个数字列表(如分数或特征)之间的夹角来检查它们的相似程度。如果夹角很小,意味着列表非常相似,即使它们的长度不同。它可以帮助您了解两个事物的密切关系,基于它们的方向。
现在让我们详细了解它们的工作原理。
# 欧几里得距离
欧几里得距离量化了多维空间中两点之间的距离,通过测量它们之间的分离程度和基于空间距离的相似性。这种度量在在线购物平台上尤为有价值,该平台根据用户的浏览和购买习惯向客户推荐产品。在这里,每个产品可以被描绘为多维空间中的一个点,其中不同的维度代表价格、类别和用户评级等方面。
当用户查看或购买特定商品时,系统会计算产品向量之间的欧几里得距离。当两个产品的距离较近时,它们被认为更相似,这有助于系统推荐与用户偏好密切匹配的商品。
# 公式:
二维空间中两点A(x1,y1)和B(x2,y2)之间的欧几里得距离d如下所示:
对于n维空间,公式推广为:
该公式通过对两个点的每个对应维度的差的平方求和,然后取平方根来计算距离。本质上,它衡量了两个点在直线上的距离有多远,这是一种评估相似性的简单方法。
# 代码示例
现在让我们编写一个生成图形以计算欧几里得距离的示例:
import numpy as np
import matplotlib.pyplot as plt
# 定义二维空间中的两个点
point_A = np.array([1, 2])
point_B = np.array([2, 3])
# 计算欧几里得距离
euclidean_distance = np.linalg.norm(point_A - point_B)
# 创建图形和轴
fig, ax = plt.subplots(figsize=(8, 8))
# 绘制点
ax.quiver(0, 0, point_A[0], point_A[1], angles='xy', scale_units='xy', scale=1, color='r', label='Point A (1, 2)')
ax.quiver(0, 0, point_B[0], point_B[1], angles='xy', scale_units='xy', scale=1, color='b', label='Point B (2, 3)')
# 设置图形的限制
ax.set_xlim(0, 3)
ax.set_ylim(0, 4)
# 添加网格
ax.grid()
# 添加标签
ax.annotate('A', point_A, textcoords="offset points", xytext=(-10,10), ha='center', fontsize=12)
ax.annotate('B', point_B, textcoords="offset points", xytext=(10,-10), ha='center', fontsize=12)
# 绘制表示欧几里得距离的线
ax.plot([point_A[0], point_B[0]], [point_A[1], point_B[1]], 'k--', label='Euclidean Distance')
# 添加图例
ax.legend()
# 添加标题和标签
ax.set_title(f'Euclidean Distance: {euclidean_distance:.2f}')
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis')
# 显示图形
plt.show()
执行此代码后,将生成以下输出。
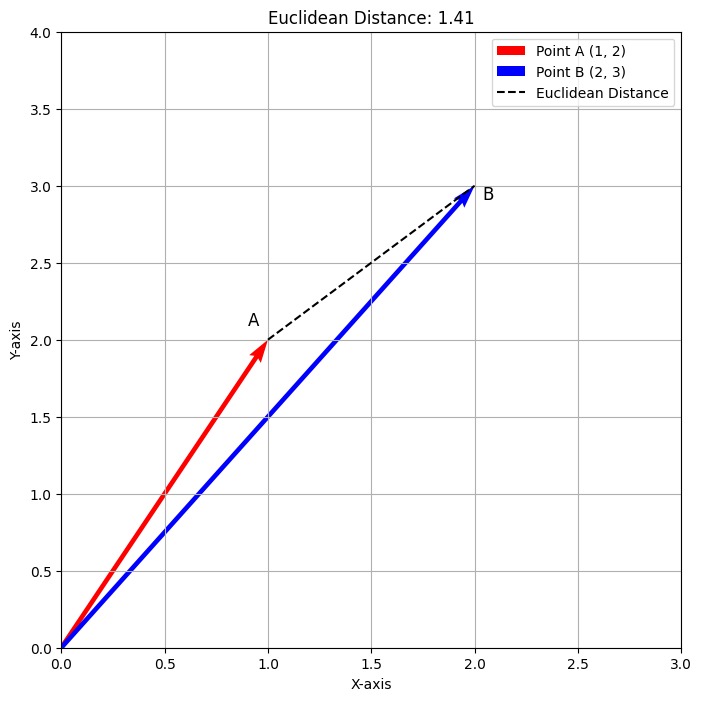
上图显示了点A(1,2)和B(2,3)之间的欧几里得距离。红色向量表示点A,蓝色向量表示点B,虚线表示距离,约为1.41。这个可视化清晰地表示了欧几里得距离如何测量两点之间的直线路径。
# 余弦相似度
余弦相似度是一种用于衡量两个向量相似程度的度量标准,无论它们的大小如何。它量化了n维空间中两个非零向量之间的夹角的余弦值,提供了它们方向上的相似性。这种度量在推荐系统中特别有用,例如Netflix或Spotify等内容平台中使用的推荐系统,它帮助根据用户的偏好推荐电影或歌曲。在这种情况下,每个项目(例如电影或歌曲)可以表示为特征向量,例如流派、评级和用户互动。
当用户与特定项目进行交互时,系统会计算相应项目向量之间的余弦相似度。如果余弦值接近1,则表示相似度很高,有助于平台推荐与用户兴趣相符的项目。
# 公式:
两个向量A和B之间的余弦相似度S计算如下:
其中:
- A⋅B 是向量的点积。
- ∥A∥ 和 ∥B∥ 是向量的模(或范数)。
该公式计算了两个向量之间夹角的余弦值,从而根据方向而不是大小来衡量它们的相似性。
# 代码示例
现在让我们编写一个计算余弦相似度并可视化向量的示例:
import numpy as np
import matplotlib.pyplot as plt
# 定义二维空间中的两个向量
vector_A = np.array([1, 2])
vector_B = np.array([2, 3])
# 计算余弦相似度
dot_product = np.dot(vector_A, vector_B)
norm_A = np.linalg.norm(vector_A)
norm_B = np.linalg.norm(vector_B)
cosine_similarity = dot_product / (norm_A * norm_B)
# 创建图形和轴
fig, ax = plt.subplots(figsize=(8, 8))
# 绘制向量
ax.quiver(0, 0, vector_A[0], vector_A[1], angles='xy', scale_units='xy', scale=1, color='r', label='Vector A (1, 2)')
ax.quiver(0, 0, vector_B[0], vector_B[1], angles='xy', scale_units='xy', scale=1, color='b', label='Vector B (2, 3)')
# 绘制向量之间的角度
angle_start = np.array([vector_A[0] * 0.7, vector_A[1] * 0.7])
angle_end = np.array([vector_B[0] * 0.7, vector_B[1] * 0.7])
ax.plot([angle_start[0], angle_end[0]], [angle_start[1], angle_end[1]], 'k--', color='gray')
# 注释角度和余弦相似度
ax.text(0.5, 0.5, f'Cosine Similarity: {cosine_similarity:.2f}', fontsize=12, color='black', ha='center')
# 设置图形的限制
ax.set_xlim(0, 3)
ax.set_ylim(0, 4)
# 添加网格
ax.grid()
# 添加向量的注释
ax.annotate('A', vector_A, textcoords="offset points", xytext=(-10, 10), ha='center', fontsize=12)
ax.annotate('B', vector_B, textcoords="offset points", xytext=(10, -10), ha='center', fontsize=12)
# 添加图例
ax.legend()
# 添加标题和标签
ax.set_title('Cosine Similarity Visualization')
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis')
# 显示图形
plt.show()
执行此代码后,将生成以下输出。
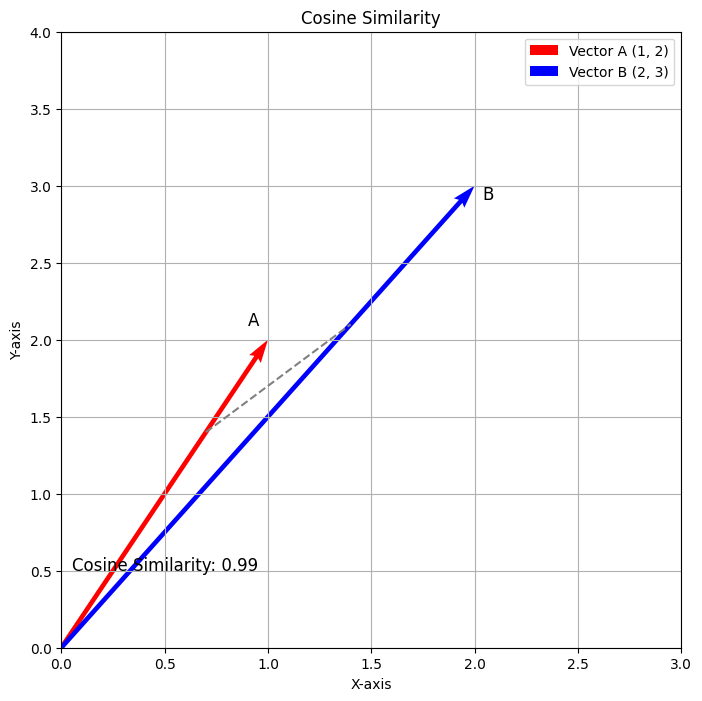
上图显示了向量A(1,2)和B(2,3)之间的余弦相似度。红色向量表示向量A,蓝色向量表示向量B。虚线表示两个向量之间的角度,计算得到的余弦相似度约为0.98。这个可视化有效地表示了余弦相似度如何测量两个向量之间的方向关系。
# 相似性度量在向量数据库中的应用
向量数据库在推荐引擎和基于AI的分析中发挥着关键作用,通过将非结构化数据转化为高维向量,实现高效的相似性搜索。欧几里得距离和余弦相似度等定量度量用于比较这些向量,使系统能够提供适当的内容推荐或识别异常。例如,推荐系统将用户喜好与项目向量配对,提供定制化的推荐。
MyScale (opens new window)利用这些度量标准来支持其MSTG(多尺度树图) (opens new window)算法,该算法结合了树和基于图的结构,以在大型、经过筛选的数据集中执行高效的向量搜索。当筛选条件严格时,MSTG在处理筛选搜索方面特别有效,优于HNSW等其他算法,从而实现更快、更精确的最近邻搜索。
MyScale中的度量类型允许用户在数据的性质和期望的结果之间切换欧几里得(L2)、余弦或**内积(IP)**距离度量。例如,在推荐系统或自然语言处理任务中,经常使用余弦相似度来匹配向量,而对于需要空间接近性的任务(如图像或物体检测),则更倾向于使用欧几里得距离。
通过将这些度量标准纳入其MSTG算法中,MyScale优化了对各种数据模态的向量搜索,使其非常适用于需要快速、准确和可扩展的基于AI的分析。
# 结论
总之,欧几里得距离和余弦相似度等相似性度量在机器学习、推荐系统和AI应用中发挥着关键作用。通过比较表示数据点的向量,这些度量标准使系统能够发现对象之间的联系,从而提供个性化的建议或识别数据中的模式。欧几里得距离计算点之间的线性距离,而余弦相似度则检查方向相关性,每种度量标准在特定场景下都有不同的优势。
MyScale通过其创新的MSTG算法增强了这些相似性度量的效果,该算法优化了相似性搜索的速度和准确性。通过集成树和图结构,MSTG加速了搜索过程,即使在复杂的筛选数据下也能实现快速、精确的最近邻搜索,使MyScale成为高性能的基于AI的分析、大规模数据处理和精确、高效的向量搜索的强大解决方案。




