在我们之前对对比学习 (opens new window)的探索中,我们揭示了模型如何通过在嵌入空间中将相似的数据聚集在一起并将不相似的数据推开来学习区分相似和不相似数据。我们讨论了一些方法,如SimCLR (opens new window)、MoCo (opens new window)和CLIP (opens new window),它们在自监督学习 (opens new window)方面取得了显著的进展。
在度量学习的旅程中,让我们来谈谈Triplet Loss。它建立在对比学习的原理之上,在需要进行细粒度区分的任务(如人脸识别、图像检索和签名验证)中起着关键作用。
# 度量学习
在我们深入了解Triplet Loss之前,了解度量学习很重要。度量学习是一种机器学习方法,专注于学习一种测量数据点之间相似性的距离函数(或度量)。其核心思想很简单:
- 相似的数据点应该靠近在嵌入空间中。
- 不相似的数据点应该远离。
我们使用机器学习模型生成嵌入,然后训练模型使相似的数据点之间的距离最小化,同时使属于不同类别或标签的数据点之间的距离最大化。
# 常见的距离度量
在谈到距离时,距离的选择取决于用户。可以是欧氏距离、曼哈顿距离或一些高级距离度量。一些常用的距离包括:
- 闵可夫斯基距离 - 闵可夫斯基距离通过计算p范数来推广基于范数的距离,其中
- 余弦相似度 - 余弦相似度基于向量的点积。它考虑到平行向量的相似度为1(cos 0º),垂直向量的相似度为0(cos 90º),而相反向量的相似度为-1(cos 180º)。
- 曼哈顿距离:也称为城市街区距离或L1距离,曼哈顿距离计算两点坐标之间的绝对差值的总和。在处理类似网格路径的情况或无法进行对角线移动的情况下特别有用。
- 杰卡德距离 - 杰卡德距离通过计算匹配元素与总元素的比率来衡量两个组(集合)之间的相似性(或不相似性)。
- 马氏距离 - 马氏距离是一种考虑数据分布的独特度量。它定义为:
这里
# Triplet loss是什么?
现在让我们回到主题。Triplet loss基于一个简单的原理工作。我们选择嵌入空间中的一个点(通常称为锚点),分别选择一个正样本和一个负样本。不可避免地,我们希望最大化与负样本的距离,并最小化与正样本的距离。
这里
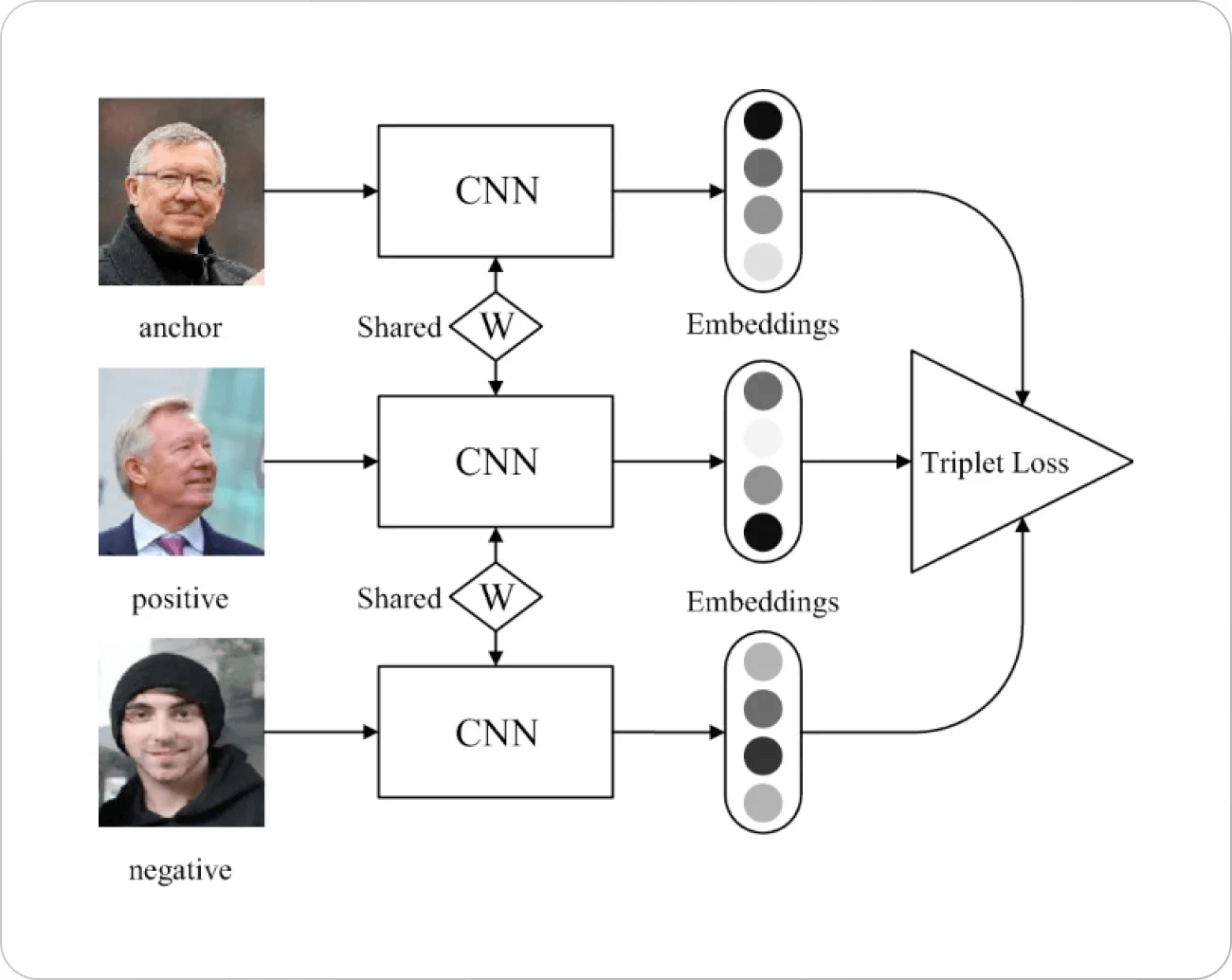
图片来源:Springer Paper
Triplet loss的动机背后有一些背景。早期的人脸识别损失函数(主要基于
# Triplet Loss的工作原理
想象一下在嵌入空间中绘制数据点。使用Triplet Loss:
- 锚点和正样本(同一类别)被拉近。
- 锚点和负样本(不同类别)被推开。
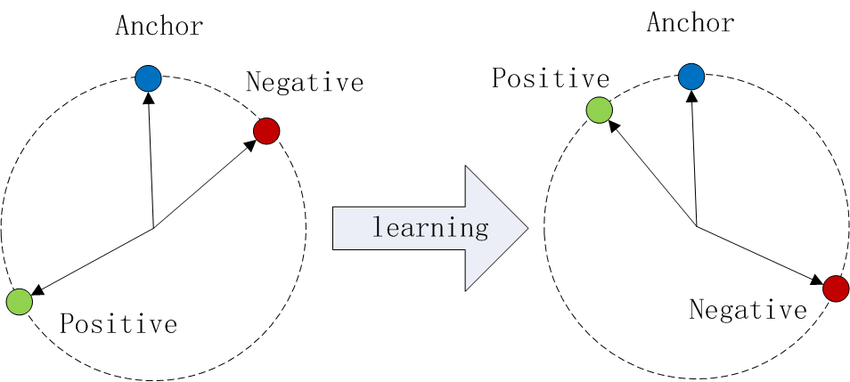
图片来源:Wikipedia
这个过程为每个类别创建了独特的聚类,提高了模型区分它们的能力。
# 间隔α
间隔α是一个超参数,它设置了正样本和负样本相对于锚点之间的最小期望距离。它防止模型将所有嵌入都折叠到同一个点上,并鼓励类别之间有意义的分离。
α α
选择适当的间隔对于有效的训练至关重要。
# 为什么使用Triplet Loss?
Triplet Loss在以下情况下特别有用:
- 需要细粒度区分:在需要捕捉微小差异的任务中,如人脸识别。
- 类别分布不平衡:它关注相对距离而不是嵌入空间中的绝对位置。
- 学习区分特征:它强制模型关注区分类别的特征。
# 三元组挖掘
Triplet loss的确带来了一些成本,因为我们需要将每个点与所有正样本和负样本进行比较,这意味着随着训练数据的增长,训练变得不可行,导致最坏情况下的复杂度为
为了解决这个问题,我们可以巧妙地找到难例正样本和难例负样本。例如,在人脸识别中,难例正样本可以是同一个人的照片,但在非常不同的环境中(如光照、服装、姿势等),类似地,难例负样本可以是在相似环境中的不同人。找到这些难例正样本和难例负样本的过程称为挖掘。与其他涉及大量数据的算法类似,它也是在小批量中进行的。
# 挑战
找到这些难例正样本和负样本是一个明确的问题,但在训练后期还会出现更大的挑战。
- 选择合适的批量大小:样本太少会导致数据的表示不足,从而导致难例不足。另一方面,批量大小太大会限制计算资源(主要是GPU内存限制)。
- 难度的程度:首先呈现难例,特别是难例负样本,会导致训练不佳[1],这是可以理解的。因此,需要搜索一些负样本,使得
换句话说,我们选择不完全难(不等式确保它们不位于正样本的边缘上)的负样本
注意:
课程学习的概念与选择适当的难度程度非常相关。这个技术的名字正如其所示,受到学校学习的启发。使用这种技术,我们首先向模型呈现最简单的例子(如黑白对比样本),然后逐渐提高难度。反课程学习则相反,首先呈现最困难的例子,然后逐渐放松。2021年,研究人员[3]进行了一项广泛的研究,发现课程学习在某些情况下可能是有帮助的,特别是在噪声数据和有限训练时间的情况下。
在线生成与离线生成:另一个选择是是否提前生成所有三元组(离线生成)还是动态生成它们。两种选项都有各自的优点和缺点。离线生成允许我们正常生成批次,而在线生成是自适应的。在生成难例时可能会有一些开销。
# Triplet Loss和对比学习
Triplet loss和对比学习都旨在通过使嵌入更接近所需类别(即距离更小)并远离异常值来进行学习,因此它们经常被视为相同的。虽然它们的目的相同,但它们之间存在明显的区别,对比损失将每个样本与一批正样本和负样本进行对比,而三元组损失(理论上)对所有可能的三元组进行对比。
由于对比学习不需要生成所有的三元组(或对),因此它的计算速度比三元组损失的实现要快得多。然而,在大多数情况下,三元组损失具有更好的准确性。
对比学习和Triplet Loss的区别
数据分组:
- 对比学习:操作样本对(正样本或负样本)。
- Triplet Loss:操作样本三元组(锚点、正样本、负样本)。
损失机制:
- 对比学习:使用二进制决策来判断样本是否相似或不相似。
- Triplet Loss:关注锚点-正样本和锚点-负样本之间的相对距离,确保正样本比负样本更接近锚点。
灵活性:
- 对比学习:在计算上更简单,因为它只涉及样本对,但在多个负样本接近锚点的复杂情况下可能不够有效。
- Triplet Loss:更复杂,但可以更好地控制嵌入空间,因为它直接优化相对距离。
训练复杂性:
- 对比学习:通常实现较简单,因为只需要样本对。
- Triplet Loss:更复杂,因为它需要精心选择的三元组(通常使用难例负样本来提高性能)。
# 实现
我们可以通过选择锚点(参考点)和正负样本来实现它。在这里,我们将使用闵可夫斯基距离 - 即将范数的阶数的选择留给用户。
import torch
import torch.nn as nn
class TripletLoss(nn.Module):
def __init__(self, margin=1.0):
super(TripletLoss, self).__init__()
self.margin = margin
def forward(self, anchor, positive, negative, norm_order):
pos_dist = torch.norm(anchor - positive, p=norm_order, dim=1)
neg_dist = torch.norm(anchor - negative, p=norm_order, dim=1)
loss = torch.mean(torch.clamp(pos_dist - neg_dist + self.margin, min=0.0))
return loss
# 最佳实践
使用Triplet Loss的一些最佳实践包括:
- 正常的欧氏距离比平方欧氏距离有更好的结果。
- 归一化(如批量归一化或层归一化)通常在训练中没有帮助。
- 一个最佳的批量大小([1]在大多数实验中使用了约1800个)。
# 结论
Triplet Loss是度量学习中的一种有价值的工具,通过关注数据点之间的相对距离,帮助模型区分相似和不相似的数据点。基于对比学习的思想,它特别适用于需要对类别之间进行微小区分的任务。
通过将Triplet Loss纳入我们的模型中,我们可以教会它们以更精细的方式识别模式,为计算机视觉、语言处理等领域的应用开辟了令人兴奋的可能性。
# 参考资料
- Schroff等人(CVPR 2015)FaceNet: A Unified Embedding for Face Recognition and Clustering
- Hermans等人(2017),In Defense of the Triplet Loss for Person Re-Identification
- Wu等人(ICLR 2021),When Do Curricula Work?




